Next: About this document ...
Physics 215A
Midterm
Fall, 1999
Problem 1
Let
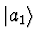 and
and
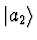 be two states with
be two states with
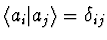 .
A Hamiltonian is given by
.
A Hamiltonian is given by
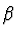 is a real number.
is a real number.
- a.
- Find the eigenvectors of H as combinations of the two
states
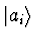 and their corresponding eigenvalues.
and their corresponding eigenvalues.
- b.
- Suppose at t=0 the system is in the state
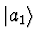 .
Write down the
state vector for t>0.
.
Write down the
state vector for t>0.
- c.
- What is the probability of finding the system in state
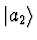 at
time t>0?
at
time t>0?
Problem 2
Sometimes it is convenient to approximate a situation by using a complex
potential
with VR and VI real. We find that
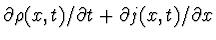 is no longer equal to zero. What is it equal
to?
is no longer equal to zero. What is it equal
to?
Problem 3
- a.
- If
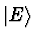 is an eigenstate of the Hamiltonian H, show
that
is an eigenstate of the Hamiltonian H, show
that
for any operator 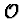 (not depending explicitly on time).
(not depending explicitly on time).
- b.
- For
evaluate
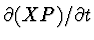 .
.
- c.
- Using the two results above we can show that
where c is a constant. Derive the above and find c?



Next: About this document ...
Myron Bander
2000-03-22