


Next: About this document ...
Physics 215A
Fall 2000
In the next several problems the symbol
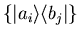 represents the
process of accepting the system in state
represents the
process of accepting the system in state 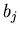 and turning it into the
state
and turning it into the
state 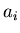 . Schwinger and Gottfried use the symbol
. Schwinger and Gottfried use the symbol 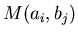 .
.
Problem 1
Show that
and
Problem 2
Define
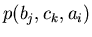 as
as
[a.] Give a physical meaning to this expression.
[b.] Show that
[c.] Discuss why in classical mechanics you would expect the equality
to hold.
Problem 3
Show that the identification
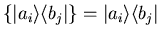 satisfies the properties we wish
satisfies the properties we wish
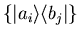 to have, namely
to have, namely
Problem 4
Show that if
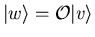 then
then
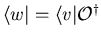 .
.
Problem 5
Show that
Problem 6
Show that for
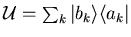 ,
,
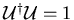 (
(
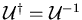 ). also, show
that in general
). also, show
that in general
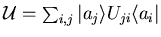 is unitary provided
is unitary provided 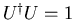 , taken as matrix
multiplication. (
, taken as matrix
multiplication. (
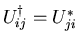 ).
).
Problem 7
Show that:
(1) The product of two unitary operators is unitary.
(2) If the trace of an operator 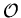 is defined as
is defined as
then
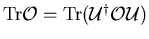 , for any
unitary
, for any
unitary 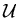 .
.
(3) If 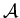 is Hermitian so is
is Hermitian so is
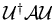 for
any unitary
for
any unitary 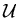
Problem 8
Remembering that the probability of obtaining 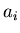 for a measurement
of
for a measurement
of 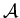 in the state
in the state 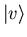 is
is
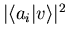 , show that
the average value for a measurement of
, show that
the average value for a measurement of 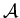 in this state is
in this state is
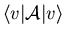
Problem 9
Find the eigenvalues and normalized eigenfunctions of the following
operator
where the vectors
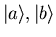 satisfy
satisfy
Problem 10
A certain operator has a 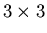 matrix representation as follows:
matrix representation as follows:
Find the normalized eigenvectors and corresponding eigenvalues. Is there
any degeneracy
Problem 11
Show that
for 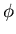 restricted to the interval
restricted to the interval
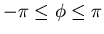 . To do this
show that
. To do this
show that 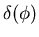 , as defined above, satisfies
, as defined above, satisfies
for the latter, do the sum over 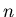 explicitly.
explicitly.
Problem 12
Relate
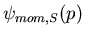 to
to 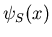 and obtain an expression for
and obtain an expression for
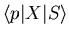 in terms of
in terms of
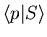 .
.
Problem 13 [20 points]
(a) Find the propagator for a free particle.
(b) Suppose that
find 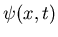 .
.
Problem 14
For the potential 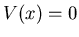 for
for 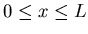 and
and 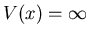 otherwise,
calculate
otherwise,
calculate
![$\langle S,t\vert[X-(L/2)]\vert S,t\rangle$](img50.png) for the case where
for the case where
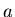 and
and 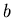 are complex numbers.
are complex numbers.
Problem 15
[a.] Show that if 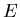 is nondegenerate the eigenfunction of the
Schrödinger equation,
is nondegenerate the eigenfunction of the
Schrödinger equation,
can be chosen to be real.
[b.] Show that the same holds even if 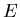 is degenerate.
is degenerate.
Problem 16
If in the above problem 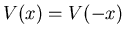 , show that the eigenfunctions can be
chosen to be symmetric or antisymmetric as
, show that the eigenfunctions can be
chosen to be symmetric or antisymmetric as
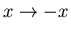 .
.
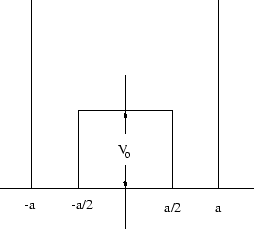
Problem 17 [20 points]
For the potential illustrated below,
namely 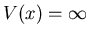 for
for 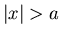 ,
, 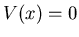 for
for 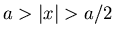 and
and
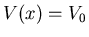 for
for 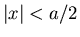 set up the procedure to find the energy
eigenvalues and the corresponding wave functions for both the odd and
even parity situations and for energies greater or smaller than
set up the procedure to find the energy
eigenvalues and the corresponding wave functions for both the odd and
even parity situations and for energies greater or smaller than 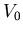 .
Namely:
.
Namely:
a. Write down the form of the wave functions in all the regions.
b. What equations arise as a consequence of the boundary conditions?
Do not try to solve these equations.
Problem 18
(a) Calculate the following matrix elements for the harmonic oscillator:
(b) Show that the expectation value of the kinetic energy in some
state is equal to the expectation value of the potential energy in
that state.
Problem 19.
An electron near the surface of liquid helium feels a potential
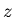 is the height above the surface and
is the height above the surface and 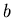 is some
parameter. Ignore the motion in the
is some
parameter. Ignore the motion in the 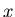 and
and 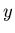 directions.
directions.
- a.
- Write out the Schrödinger equation for this problem.
- b.
- What is the form of the solution of this equation for large,
positive
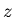 ?
?
- c.
- What is the behavior of the solution for small, positive
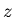 ?
?
- d.
- Combining the results of [b.] and [c.] guess (or derive) the wave
function for the ground state and find the energy of that state.
Problem 20
A particle of mass 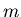 is bound in a potential
is bound in a potential 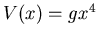 . Scale the
Schrödinger equation and determine the dependence of the energies
on
. Scale the
Schrödinger equation and determine the dependence of the energies
on 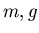 and
and 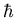 . Find numerically the energies and wave
functions of the first two even parity states and the first odd parity
state.
. Find numerically the energies and wave
functions of the first two even parity states and the first odd parity
state.
Problem 21
At 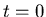 a harmonic oscillator is in the state
a harmonic oscillator is in the state
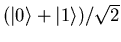 . What is the probability of finding it in the state
. What is the probability of finding it in the state
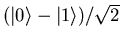 at time
at time 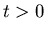 ? The frequency of the
oscillator is
? The frequency of the
oscillator is 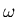 .
.
Problem 22
For the potential
with 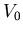 positive, find the reflection and transmission coefficients
for
positive, find the reflection and transmission coefficients
for 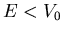 .
.
Problem 23
Sakurai, 3.1; p.242
Problem 24
In this problem you derive some useful relations for the Pauli spin
matrices.
[a.] Show that
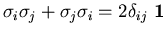 ;
;
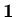 is the unit
is the unit 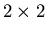 matrix.
matrix.
[b.] If  and
and 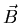 are ordinary, i.e. commuting,
vectors, show that
are ordinary, i.e. commuting,
vectors, show that
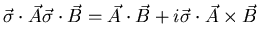 . [Use the
result in part [a.]]
. [Use the
result in part [a.]]
[c.] Show that
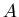 is the magnitude of
is the magnitude of  . [Hint. Expand the exponential, use
result [a.] and resum the series.]
. [Hint. Expand the exponential, use
result [a.] and resum the series.]
Problem 25
The deuteron, among other systems, has an intrinsic spin 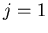 ; such
systems may be described by a three component object. Obtain an explicit
representation of the
; such
systems may be described by a three component object. Obtain an explicit
representation of the 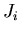 's as
's as 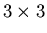 matrices.
matrices.
Problem 26
Evaluate
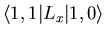 both algebraically and by doing the
integral
both algebraically and by doing the
integral
Problem 27
Sakurai, 3.17; p. 244
Problem 28
Find the energy levels, for each angular momentum state, of the three
dimensional harmonic oscillator. Each state 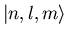 is a linear
superposition of the rectangular coordinate solutions
is a linear
superposition of the rectangular coordinate solutions
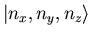 . Find explicitly
. Find explicitly
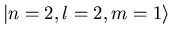 as a combination
of the
as a combination
of the
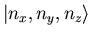 's.
's.
Problem 29
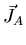 and
and 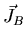 are two sets of angular momentum operators
acting on two different systems. Show that
are two sets of angular momentum operators
acting on two different systems. Show that
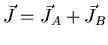 are also angular momentum operators.
are also angular momentum operators.
Problem 30
Find the eigenvalues and the ground state eigenfunction of the
two dimensional hydrogen atom
![$\left[V(r)=
-\alpha\hbar c/r\right]$](img98.png) .
.
Problem 31
The Hamiltonian for a charged particle in a magnetic field is
where
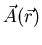 is the vector potential related to the magnetic
field by
is the vector potential related to the magnetic
field by
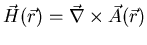 .
What are
.
What are
Compare to the classical equations of motion.
Problem 32
For the above problem find an expression for the probability current
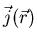 such that
such that
Problem 33
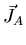 and
and 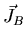 are angular momentum operators referring
to two different systems
are angular momentum operators referring
to two different systems 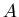 and
and 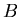 . Obtain the commutators
. Obtain the commutators
![$[J_{A,z},
{\vec J}_A\cdot{\vec J}_B]$](img106.png) ,
,
![$[J_{B,z},{\vec J}_B\cdot{\vec J}_B]$](img107.png) and
and
![$[J_{A,z}+J_{B,z},{\vec J}_A\cdot{\vec J}_B]$](img108.png) .
.
Problem 34
A spin-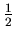 particle is placed in a magnetic field pointing along
the
particle is placed in a magnetic field pointing along
the 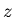 direction. The Hamiltonian is
direction. The Hamiltonian is
with
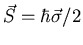 . Find and solve the equations of
motion for
. Find and solve the equations of
motion for 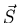 .
.
Problem 35.
The region of space for 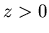 contains a magnetic field
contains a magnetic field
 . There is no field for
. There is no field for 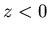 . A beam of neutral spin
one half particles with mass
. A beam of neutral spin
one half particles with mass 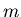 and magnetic moment
and magnetic moment
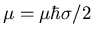 is incident from the left of the interface. (The
interaction of the magnetic moment with the magnetic field is given by
is incident from the left of the interface. (The
interaction of the magnetic moment with the magnetic field is given by
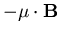 .) The beam has momentum
.) The beam has momentum 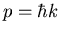 and
makes an angle
and
makes an angle 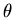 with the
with the 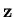 axis. Take
axis. Take 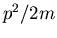 to be
greater than
to be
greater than 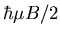 .
.
[a.] Find the wave function for the reflected and transmitted
waves for the cases where the spin is parallel and anti-parallel to the
magnetic field.
[b.] Write the wave functions for the case the incident spin
is parallel to the 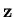 axis.
axis.
Problem 36
A spin 1/2 particle, of mass 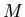 and Landé factor
and Landé factor 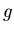 is placed in a
constant magnetic field pointing in the z direction,
is placed in a
constant magnetic field pointing in the z direction,
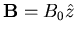 . In
addition, this system is subjected to a rotating magnetic
. In
addition, this system is subjected to a rotating magnetic
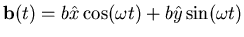 . The particle is
initially with spin up along the z direction. Find, as a function of time,
the probability of finding it with spin down.
. The particle is
initially with spin up along the z direction. Find, as a function of time,
the probability of finding it with spin down.
Problem 37.
- a.
- Two spin-
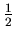 particles are at rest and initially in a
state with total spin-angular momentum zero. In term of the states
particles are at rest and initially in a
state with total spin-angular momentum zero. In term of the states
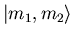 , with
, with
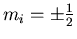 (
(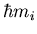 is the
is the
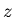 -component of the spin of particle
-component of the spin of particle 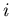 ), write out the initial state of
this two particle system.
), write out the initial state of
this two particle system.
- b.
- A Hamiltonian
acts on this system [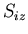 is the
is the 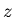 -component of spin of particle
-component of spin of particle
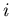 ]. As a function of time, what is the probability of finding the system
is a state with total spin-angular momentum equal to
]. As a function of time, what is the probability of finding the system
is a state with total spin-angular momentum equal to 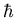 ?
?
Problem 38
[a.] Evaluate ![$[J_z,XY]$](img134.png) , where
, where 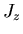 is the operator for angular momentum
in the z direction and
is the operator for angular momentum
in the z direction and 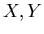 are the x and y components of the position operator.
are the x and y components of the position operator.
[b.] Using [a.], above, show that for any 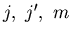 and
and 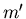
Problem 39
Some process is governed by the matrix elements
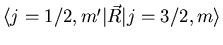 . Suppose we know
. Suppose we know
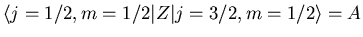 . Find all the other matrix elements of
. Find all the other matrix elements of 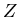 and of
and of 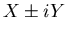 .
.



Next: About this document ...
Myron Bander
2000-09-19
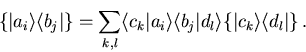
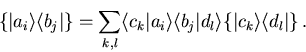
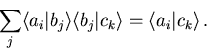
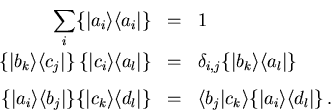
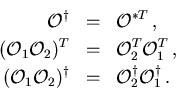
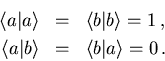
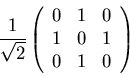
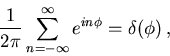
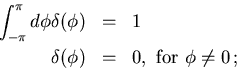
![\begin{displaymath}
\psi(x,0)=\left (\frac{1}{2\pi\sigma^2}\right )^{\frac{1}{4}...
...[-\frac{(x-x_0)^2}{4\sigma^2}+
\frac{ip_0x}{\hbar}\right ]\, ,
\end{displaymath}](img45.png)
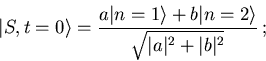
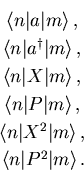
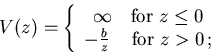
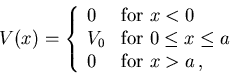
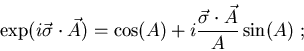
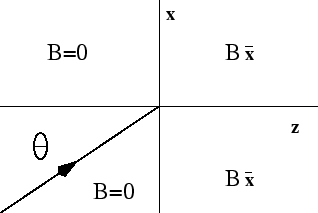
![]() axis.
axis.
![]() and Landé factor
and Landé factor ![]() is placed in a
constant magnetic field pointing in the z direction,
is placed in a
constant magnetic field pointing in the z direction,
![]() . In
addition, this system is subjected to a rotating magnetic
. In
addition, this system is subjected to a rotating magnetic
![]() . The particle is
initially with spin up along the z direction. Find, as a function of time,
the probability of finding it with spin down.
. The particle is
initially with spin up along the z direction. Find, as a function of time,
the probability of finding it with spin down.