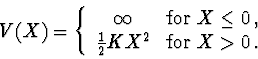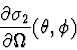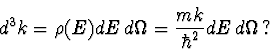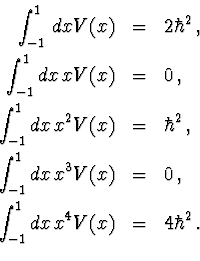Next: About this document ...
Physics 215B
Final
Winter, 2000
Open book, open notes.
Problem 1 [15 points]
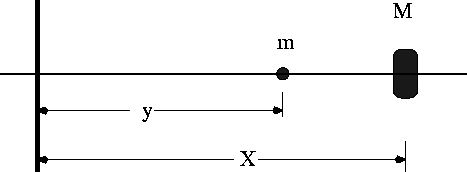
A particle of mass M moves in one dimension acted on by the potential
A second particle, of mass m, with m<<M and coordinates y moves
between the origin and X (the second particle cannot go to the right of
the first one).
[a.] Use the Born-Oppenheimer approximation to obtain the
effective potential seen by the heavy particle; the light particle is in
its lowest state. Make a sketch of this potential. [Hint: Don't be fancy -
this problem does not involve Berry's phase.]
[b.] Find the approximate low lying spectrum of the heavy
particle.
Problem 2 [10 points]
The differential cross section, in the Born approximation, for a particle
scattering off some potential
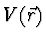 is known,
is known,
What is the differential cross section
for scattering this particle off two such potentials located at
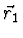 and
and
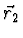 ,
(the potential, now, is
,
(the potential, now, is
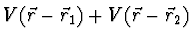 )?
)?
Problem 3 [10 points]
An atom in an excited state decays into the ground state by emitting a
photon (neglect complications due to photon polarization). The matrix
element for this process is taken to be constant,
The difference in energies of the excited and ground states is 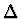 .
For a photon of momentum
.
For a photon of momentum 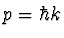 the energy is
the energy is
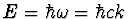 (c is the velocity of light).
(c is the velocity of light).
[a.] Derive an expression for the density of states of the photon, i.e. what is
the analog for the photon of the massive particle density of states
[b.] What is the lifetime of the excited state?
Problem 4 [15 points]
A particle of mass m=1 is moving in a one dimensional potential
V(x).
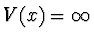 for |x|>1 and has some shape for
for |x|>1 and has some shape for
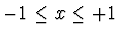 .
We know the following moments of V(x):
.
We know the following moments of V(x):
Using the above information, guess a reasonable approximate wave function
and obtain an upper bound for the ground state energy of this system.



Next: About this document ...
Myron Bander
2000-03-22