


Next: Post-Analysis
Up: Solution of the Black
Previous: Conversion of the Black-Scholes
We now use the Green's function for the Diffusion or
Heat equation[4], which is the solution to that
equation for a point (or delta function) source at point
z' at time t'=0
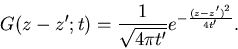 |
(19) |
The verification of this Green's function solution is shown in
Appendix A.
The Green's function shows the Gaussian diffusion of the pointlike input with
distance from the input (z-z') increasing as the square root of
the time t', as in a random walk.
We can use the Green's function
to write the solution for
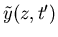 in terms of
summing over its input values at points z'on the boundary at the initial time t'=0
in terms of
summing over its input values at points z'on the boundary at the initial time t'=0
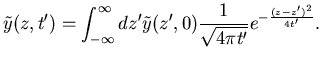 |
|
|
(20) |
Putting in the initial condtions at t'=0, where
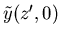 vanishes for negative z', gives
vanishes for negative z', gives
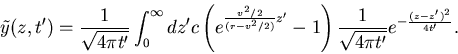 |
(21) |
To do the integral we change the variable to
| q |
= |
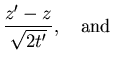 |
(22) |
| dz' |
= |
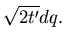 |
(23) |
The lower limit on the q integral is now
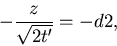 |
(24) |
where substitution gives the dimensionless
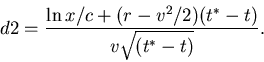 |
(25) |
In the first term we now complete the square to
get a new variable
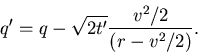 |
(26) |
The new lower limit on q' in the first term is now -d1 where
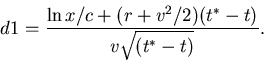 |
(27) |
After completing the square on the first term, the exponent simplifies
to
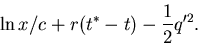 |
(28) |
Both integrals are now related to the Cumulative Distribution
Function of the Normal Distribution
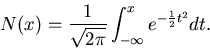 |
(29) |
If we change t to -t in the above integral and
invert the limits we get the form of our integrals
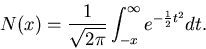 |
(30) |
We now have our solution for the canonical 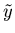
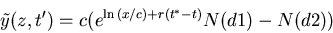 |
(31) |
Finally, we use the facts that
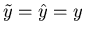 , and that
, and that
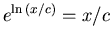 , and the conversion
, and the conversion
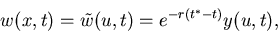 |
(32) |
to get the Black-Scholes solution
|
w(x,t) = x N(d1)-c e-r(t*-t)N(d2).
|
(33) |



Next: Post-Analysis
Up: Solution of the Black
Previous: Conversion of the Black-Scholes
Dennis Silverman
1999-05-20
![]() in terms of
summing over its input values at points z'on the boundary at the initial time t'=0
in terms of
summing over its input values at points z'on the boundary at the initial time t'=0
![]() , and that
, and that
![]() , and the conversion
, and the conversion