The three-glider system, with identical masses $m$ and spring constants $k$, will have three normal modes characterized by the angular frequencies:

$$\{ \omega_1 ^2, \omega_2 ^2, \omega_3 ^2\} = \left\{ (2-\sqrt{2})\frac{k}{m}, 2\frac{k}{m}, (2+\sqrt{2})\frac{k}{m}, \right\} $$

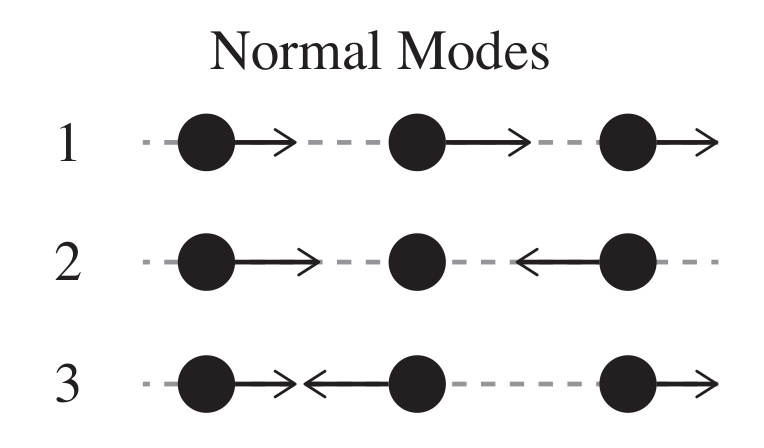
Mode 2 is the easiest to understand, since the middle glider remains stationary as the outer gliders oscillate about it, out of phase, at frequency $\omega_2$. This is conceptually obvious since each outer mass behaves as an independent oscillator attached to two springs with effective spring constant $2k$.

In Mode 1, all three gliders move in phase, at $\omega_1$, but the middle glider has a displacement amplitude $\sqrt{2}$ greater than both of the outer gliders.

Mode 3 has the outer gliders moving out of phase with the middle glider. All three gliders oscillate in simple harmonic motion at $\omega_3$, and again the middle glider has displacement amplitude $\sqrt{2}$ greater than both of the outer gliders.