The basic object of FDM is solve the harmonic inversion problem, i.e., fitting the time signal to the sum of sinusoids. This is a very difficult nonlinear fitting problem, especially when the signal contains thousands of peaks and is noisy (which is typical for NMR signals). People have devoted a lot of efforts in developing various methods such as Linear Prediction (LP). However, only very limited success has been achieved until the invention of FDM. What makes FDM special is the following: FDM solves the original large and ill-conditioned nonlinear fitting problem by converting it into pure linear algebra problems of diagonalizing some small data matrices in the frequency domain. For more detailed description of FDM, please refer to the review paper by Dr. Mandelshtam (very strongly recommended, download the preprint (PostScript file, 1254K) or read from the journal website). Some important facts of FDM are listed below.
- 1) The key assumptions of FDM: Besides assuming that the signal can
be described as the sum of sinusoids, it is also assumed that the signal
can be associated with some autocorrelation function of a fictitious dynamic
system, which is described by an effective evolution operator and some
"initial state". Mathematically, it means that, C(t) = (F0 | U(t) F0), where
F0 is the "initial state", U(t) = Exp(-i W t) is the effective evolution
operator. Then it turns out that fitting the signal to a summation of sinusoids
is equivalent to diagonalize the evolution operator U(t). The complex
frequencies (peak position and width) can be obtained from the
eigenvalues of U(t), and the complex amplitudes (peak integral and phase) from
the eigenvectors.
2) Fourier-type Basis: Even though the evolution operator (see previous paragraph) are not explicitly available, its matrix representations in an appropriately chosen basis set are completely determined by the measured time signal. Moreover and most importantly, when a narrow band Fourier-type basis is used, the resulting matrices are diagonally dominant with decaying off-diagonal elements. So that we can block diagonalize the matrices and avoid the problem of diagonalizing unfavorably huge matrices.
3) Green function approach: In multi-dimensional cases, it requires simultaneous diagonalization of two or more data matrices if one extends the 1D FDM in a primitive way. However, because practically the signal contains noise and local spectral windows are used, it is very difficult, if not impossible, to simultaneously diagonalize these matrices. Instead, a Green function approach is proposed to construct the multidimensional spectra directly (see Ref. 2), which makes the algorithm more stable and applicable to noisy signals.
4) Regularization: Regularization is very important for obtaining stable results, especially in multidimensional FDM. The matrices we deal with in FDM are typically singular and need to be regularized before we diagonalize them. There are various ways of applying regularization, among which FDM2K (3) is particularly efficient. However, more details still need to be further studied.
Current Status of FDM
The 1D FDM is now basically a well-developed method, which is generally reliable, sufficiently fast and can often deliver resolutions beyond the FT uncertainty principle. However, the difficulties associated with the construction of a meaningful line list for data of poor quality exist. These difficulties are not associated with the lack of a reliable algorithm of selecting the ``genuine'' poles and throwing away the ``noise'' poles from the full list of complex eigenvalues, but are rather conceptual caused by the ambiguity of the line list for a general data that does not fit any particular parametric form.
In mutlidimensional cases, we have made several important advances since FDM was first invented, such as the Green's Function approach and regularizations of FDM. The multidimensional spectra cannot be generally constructed from the multidimensional line list as the latter is very hard to obtain. Fortunately, various spectra can be obtained by avoiding the line list construction and using the Green's Function approach. It allows to construct various types of spectra including absorption-mode spectra, non-trivial spectral projections. The main computational problem is that one typically deals with very ill-conditioned matrices causing the spectrum to be very unstable with respect to the FDM parameters and small variations of the input data. Thus, unlike the 1D case, there are major problems to be solved in the multidimensional versions of FDM and RRT. Clearly, the key issue of multi-D FDM is to find a general computationally inexpensive and robust procedure that could be applied to regularize the FDM equations. At the present stage the problem is solved only partially.
FDM has found many applications in diverse fields and in particular for processing NMR time signals. In collaboration with Shaka Group at UCI, we are developing various new NMR experiments which can make better use of high resolving power of FDM. FDM will greatly improve a whole host of useful NMR experiments, with the most exciting applications yet to come.
FDM is also a very powerful signal processing technique for quantum dynamics calculations. A few good examples are harmonic inversion of cross-correlated semiclassical signals (5), and the computation of bound and resonance spectra of small molecules (6).
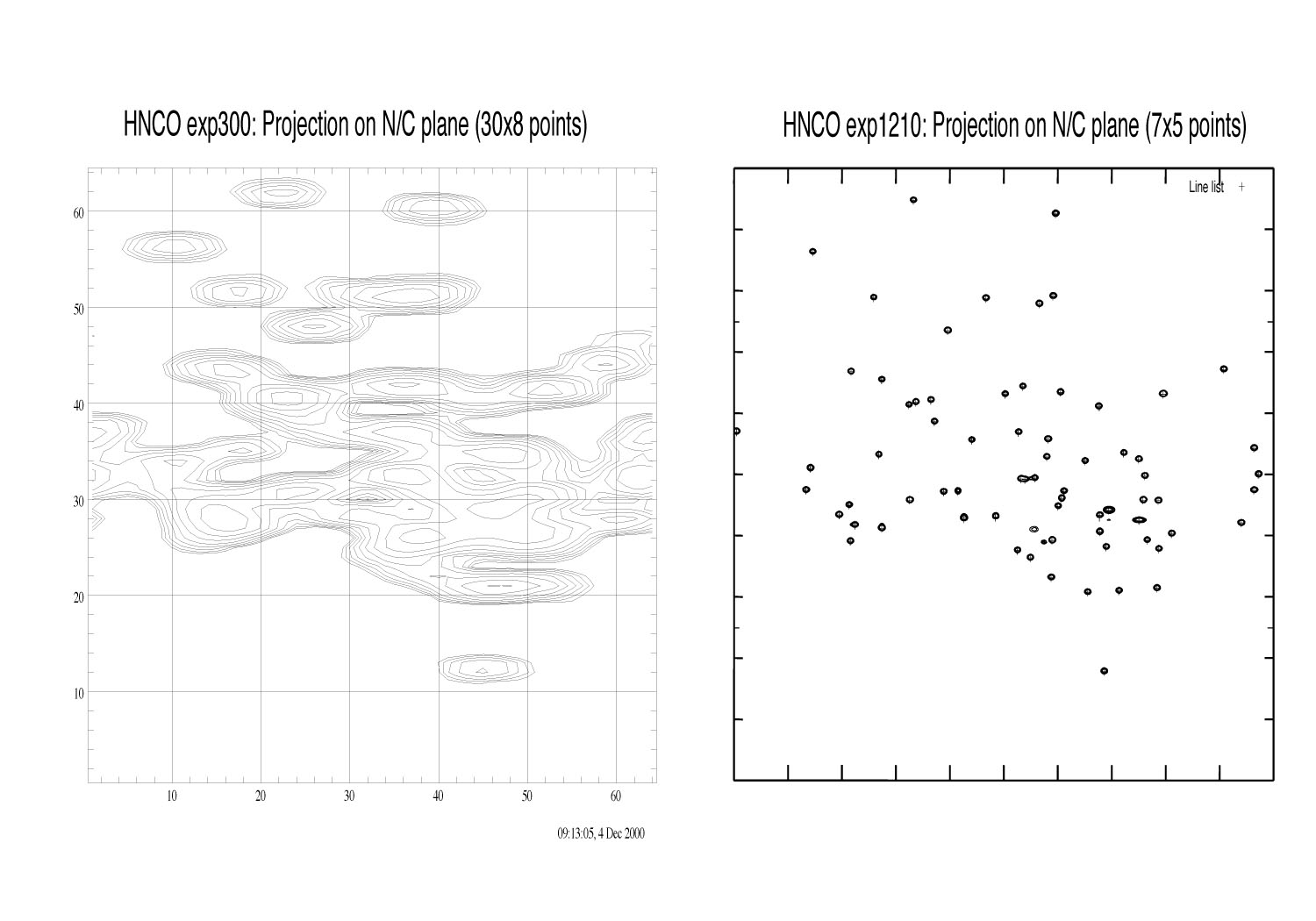
An Example: Shown below is a comparison of FT and FDM2K using a double constant time HNCO NMR signal (4) of human Ubiquitin (100% 13C/15N enriched). The resolution enhancement is enormous! As the double constant time dimensions ensure Lorentzian lineshape, we are even able to obtain a 3D "line list"(shown as "+" in the FDM spectrum)! This is the most recent result and more investigations are still to be done considering stability of the algorithm and reliability of the results in different circumstances.
1. M. R. Wall and D. Neuhauser, J. Chem. Phys.
102,
4429 (1995).
2. V. A. Mandelshtam, Prog. in Nucl. Magn. Reson.
Spec, 38, 159-196(2001).
3. J. Chen, V. A. Mandelstham and A. J. Shaka, J.
Magn. Reson. 146, 368 (2000).
4. Thanks to Dr. Daniel Nietlispach at University of
Cambridge for providing the CT-HNCO signals.
5. J. Weiss, R. Schinke and V. A. Mandelshtam, J.
Chem. Phys. 113, 4588 (2000)
6. V. A. Mandelshtam and M. Ovchinnikov, J . Chem.
Phys. 108, 9206(1998).