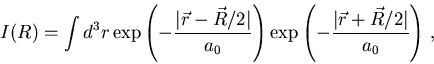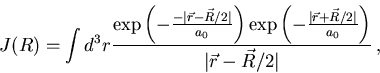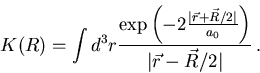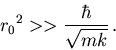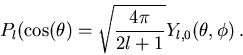Next: About this document ...
Physics 215B
Winter 2000
Problem 1
Suppose that the Coulomb potential in the hydrogen atom
were modified to a screened one (Yukawa potential)
The parameter 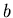 is much larger than the Bohr radius
is much larger than the Bohr radius 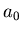 . Using
perturbation theory, find to lowest order in
. Using
perturbation theory, find to lowest order in 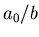 the splitting
between the S and P states of the
the splitting
between the S and P states of the 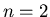 level of hydrogen.
level of hydrogen.
Ignore the fact that the  and
and 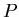 levels are degenearate and use
non-degenerate perturbation techniques. A useful formula:
levels are degenearate and use
non-degenerate perturbation techniques. A useful formula:
Problem 2
The ``relativistic dependence of mass on velocity'' adds a correction to
the Hamiltonian of a hydrogen atom
(This may be obtained by expanding
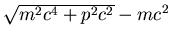 in powers of
in powers of
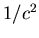 .) To first order in
.) To first order in 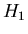 find the corrections to the energies
of the
find the corrections to the energies
of the 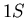 ,
, 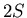 and
and 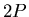 levels of hydrogen. Compare this to the
spin-orbit splitting. The calculations are easier if you write
levels of hydrogen. Compare this to the
spin-orbit splitting. The calculations are easier if you write 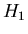 as
as
and expand out the squared term.
Problem 3
Consider a ``perturbed'' one dimensional harmonic oscillator
This problem can be solved exactly.
Nevertheless, find, to second order in 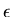 , the corrected
energy levels and compare to the exact solution.
, the corrected
energy levels and compare to the exact solution.
Problem 4
A perturbation 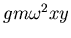 is added to the Hamiltonian for a two
dimensional harmonic oscillator
is added to the Hamiltonian for a two
dimensional harmonic oscillator
Find, to first order in 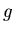 , the correction to the energy of the
(degenerate) first excited states and compare to the exact solution.
, the correction to the energy of the
(degenerate) first excited states and compare to the exact solution.
Problem 5
Sakurai, problem 5.10, p. 347
Problem 6
Two coupled oscillators are described by the Hamiltonian
with 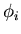 equivalent to
equivalent to 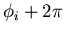 .
.
- a.
- What are the eigenfunctions and eigenvalues for the case
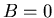 ?
?
- b.
- For
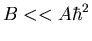 , find to lowest non-vanishing order, the
correction to the energy of the ground state.
, find to lowest non-vanishing order, the
correction to the energy of the ground state.
Problem 7
Suppose you didn't know the wave function for the ground state of the
hydrogen atom, but guessed that it is of the form
with 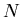 and
and 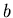 constants. Use the variational method to find these
constants.
constants. Use the variational method to find these
constants.
Problem 8
Sakurai, problem 5.21, p. 350.
Problem 9 [30 points]
Later in the quarter we shall need he ground state energy of an electron
moving in the potential of two fixed charges 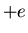 located a distance
located a distance 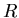 apart at coordinates
apart at coordinates 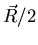 and
and 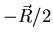 .
.
A ''good'' guess for a variational wave function is to take it to be a
superposition of hydrogenic wave functions around the two charges,
where 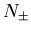 is a normalization factor. Evaluate
is a normalization factor. Evaluate
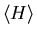 for
both wave function. Which is lower?
for
both wave function. Which is lower?
Several integrals in this problem are straight forward; you will
encounter the following ones which are more difficult:
First express your answer in terms of 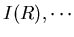 without evaluating
these explicitly. These may be evaluated by first Fourier transforming the
exponentials.
without evaluating
these explicitly. These may be evaluated by first Fourier transforming the
exponentials.
Problem 10
A particle of mass 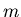 is acted on by a central three dimensional potential
is acted on by a central three dimensional potential
where 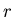 is the distance from the origin and
is the distance from the origin and
Determine the spectrum of the low lying states of this system. Discuss
and justify whatever approximations you are using. [Hint: Do not use
perturbation theory, but think of an analogy with diatomic molecules.]
Problem 11
In units where the reduced mass of some diatomic molecule is set to
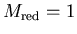 and
and 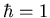 the energies of some levels are found to be
(somewhat idealized):
the energies of some levels are found to be
(somewhat idealized):
In these units, find the location of the minimum of the potential and the
second derivative of the potential at the minimum.
Problem 12
A certain attractive, three dimensional potential has a ground state with
energy 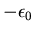 and wave function
and wave function
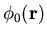 as well as an
excited state with energy
as well as an
excited state with energy 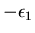 and wave function
and wave function
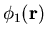 . Two identical bosons (wave function is symmetric under the
interchange of the coordinates of the two particles) of mass
. Two identical bosons (wave function is symmetric under the
interchange of the coordinates of the two particles) of mass 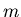 are in the
excited are in the excited state. A perturbing interaction of the form
are in the
excited are in the excited state. A perturbing interaction of the form
is turned on; 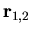 are the coordinates of the two bosons
while
are the coordinates of the two bosons
while 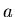 and
and 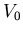 are constants with the dimensions of length and
energy respectively.
are constants with the dimensions of length and
energy respectively. 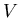 allows for the possibility of dropping one of
the bosons into the ground state and exciting the other one into the
positive energy continuum (autoionization).
allows for the possibility of dropping one of
the bosons into the ground state and exciting the other one into the
positive energy continuum (autoionization).
What is the condition on 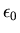 and
and 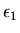 for this process to be energetically possible?
for this process to be energetically possible?
Find the expression for the rate of this process. You
may treat the continuum states as plane waves and express your answer
in term of an integral over products of wave functions.
Problem 13
A heavy nucleus, 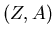 decays into a lighter one
decays into a lighter one 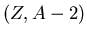 by emitting
two neutrons (ignore the symmetrization or antisymmetrization of the wave
function). The matrix element for this process is
by emitting
two neutrons (ignore the symmetrization or antisymmetrization of the wave
function). The matrix element for this process is
where 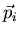 are the momenta of the neutrons and
are the momenta of the neutrons and 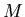 is a constant.
The energy released to the neutrons is
is a constant.
The energy released to the neutrons is  . What is the rate for this
decay?
. What is the rate for this
decay?
Problem 14
A neutron of mass 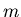 and momentum
and momentum 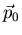 collides with a heavy
nucleus. A neutron with momentum
collides with a heavy
nucleus. A neutron with momentum 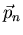 and a proton of mass
and a proton of mass 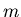 and
momentum
and
momentum 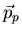 are emitted, leaving behind a nucleus with one proton
less. The matrix element for this reaction is
are emitted, leaving behind a nucleus with one proton
less. The matrix element for this reaction is
with 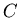 a constant. The energy released to the outgoing neutron and proton
is
a constant. The energy released to the outgoing neutron and proton
is
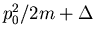 .
.
What is the cross section for the outgoing neutron to be in the energy
interval 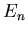 to
to 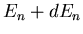 ?
?
Problem 15
Sakurai, 5.27, p. 352
Problem 16
Sakurai, 5.28, p. 353
Problem 17
Calculate, to first order in the Born approximation, the differential and
total cross section for scattering a particle of mass 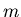 by a Yukawa
potential,
by a Yukawa
potential,
Problem 18
To first order in the Born approximation, find the differential cross section
for the scattering of a particle of charge 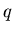 from a charge distribution
from a charge distribution
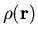 . Using this result find the differential cross section for
the case
. Using this result find the differential cross section for
the case 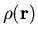 represents a total charge
represents a total charge 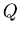 uniformly
distributed inside a sphere of radius
uniformly
distributed inside a sphere of radius 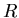 .
.
Problem 19 [20 pts]
In this problem we will obtain some of the properties of the Legendre
functions. These are related to the spherical harmonics via
and satisfy the differential equation
[a.] Show that
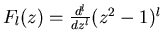 satisfies the above
equation. [Hint: Expand
satisfies the above
equation. [Hint: Expand 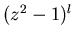 , perform all the subsequent
differentiations and show that the equation is satisfied for each power of
, perform all the subsequent
differentiations and show that the equation is satisfied for each power of
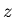 .]
.]
[b.] We will be interested in obtaining
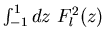 ; to do
this, first define
; to do
this, first define
and show, by considering
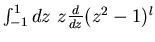 , that
, that
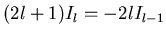 .
.
[c.] Show that
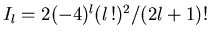 satisfies the above recursion
relation and has the correct value for
satisfies the above recursion
relation and has the correct value for 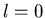 .
.
[d.] Find
[Hint: First integrate by parts till all the derivatives are on one of
the 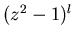 's.]
's.]
[e.] Knowing that
find the relation between 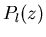 and
and 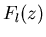 .
.
[f.] Show that 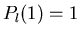 . [Hint: Write
. [Hint: Write 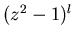 as
as
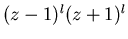 and perform some of the derivatives in the definition of
and perform some of the derivatives in the definition of 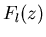 .]
.]
Problem 20
At a some small momentum 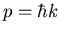 only
only 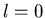 and
and 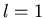 phase shifts are
important. Show that
phase shifts are
important. Show that
Problem 21
At some momentum 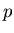 the scattering of a particle of mass
the scattering of a particle of mass 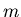 depends
only on
depends
only on  and
and 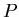 wave phase shifts (
wave phase shifts (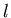 =0 and 1). Assume that we know the
total cross section,
=0 and 1). Assume that we know the
total cross section, 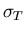 , and the differential cross section at
, and the differential cross section at
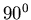 ,
,
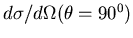 . In term of these, what is the
scattering amplitude at all angles?
. In term of these, what is the
scattering amplitude at all angles?
Problem 22
The scattering amplitude for a particle of mass 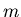 and energy
and energy 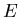 scattering off some potential is
scattering off some potential is
where 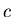 is a real number.
is a real number.
- a.
- In terms of
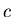 , what is the differential cross section?
, what is the differential cross section?
- b.
- What is the total cross section?
- c.
- What is
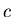 ? [Use the optical theorem.]
? [Use the optical theorem.]
Problem 23
A beam of charged particles of mass 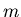 , charge
, charge 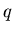 and momentum
and momentum
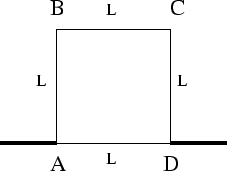
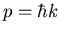 is split into two beams at point A and recombined at point
D. One beam goes directly from A to D while the other one goes along
the edges of the ABCD square. The length of each edge is L.
is split into two beams at point A and recombined at point
D. One beam goes directly from A to D while the other one goes along
the edges of the ABCD square. The length of each edge is L.
[a.] If no other potentials are present, what is the ratio of the
intensity at D to the intensity at A?
[b.] Now let there be a magnetic field perpendicular to the square. For
what values of magnetic flux, 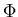 , going through the square ABCD will
the ratio of the two intensities be one?
, going through the square ABCD will
the ratio of the two intensities be one?



Next: About this document ...
Myron Bander
2000-09-19
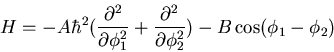
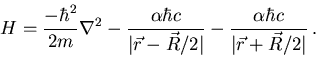
![\begin{displaymath}
\psi_{\pm}({\vec r})=N_{\pm}
\left [ \exp \left (-\frac{\ve...
...-\frac{\vert{\vec r}+{\vec R}/2\vert}{a_0}\right )\right ]\, ,
\end{displaymath}](img34.png)