The first difference we notice from the canonical equation is that
the coefficients depend on x. However, the equation is
homogeneous or invariant under the scaling of ![]() . The standard way to
simplify this and eliminate the explicit coordinate dependence is to
define a new variable
. The standard way to
simplify this and eliminate the explicit coordinate dependence is to
define a new variable
![]() , where we have scaled x by c to
make it dimensionless. Then under
, where we have scaled x by c to
make it dimensionless. Then under ![]() ,
,
![]() .
Since the equation is invariant under this, it cannot have any explicit
dependence on u in the coefficients. Changing variables to
u using
.
Since the equation is invariant under this, it cannot have any explicit
dependence on u in the coefficients. Changing variables to
u using
![]() ,
and defining
,
and defining
![]() , the derivatives become
, the derivatives become
| = | 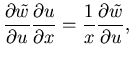 |
(7) | |
| = | 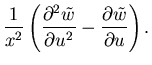 |
(8) |
Now we observe that even if
![]() is independent of
u, it still grows as ert from the
is independent of
u, it still grows as ert from the
![]() term.
Factoring this out
at the start will remove the
term.
Factoring this out
at the start will remove the
![]() term. We normalize this
behavior where the boundary condition is at t=t* by writing the
solution as
term. We normalize this
behavior where the boundary condition is at t=t* by writing the
solution as
We next scale towards a canonical form. First we scale u to
get a common coefficient for the u derivatives, and then absorb
that coefficient into a rescaling for t. The new variables are
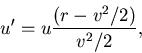 |
(12) |
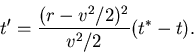 |
(13) |
| (15) |
The boundary conditions at t=t* are now
at t'=0 where z=u'. ![]() translates into
translates into ![]() .
We now use the case where
.
We now use the case where
![]() so the condition on
u translates into
so the condition on
u translates into
![]() .
The boundary conditions are then
.
The boundary conditions are then