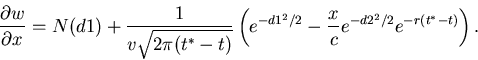Next: Green's function for the
Up: Solution of the Black
Previous: Green's Function Solution
We verify that the boundary conditions are satisfied.
For x > z,
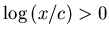 , and as
, and as
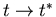 ,
,
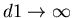 and
and
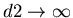 . Then both
. Then both
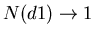 and
and
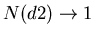 , giving
w(x,t*) = x-c as
required. For x < z,
, giving
w(x,t*) = x-c as
required. For x < z,
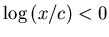 , and as
, and as 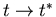 ,
,
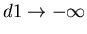 , and
, and
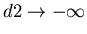 , so both N(d1) and N(d2)vanish, and
w(x,t*)=0.
, so both N(d1) and N(d2)vanish, and
w(x,t*)=0.
To find the number of call options to hold at a given time
(
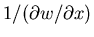 ), we calculate
), we calculate
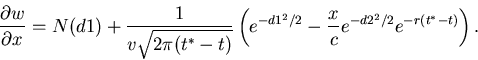 |
(34) |
If x < c, as 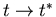 ,
,
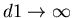 and
and
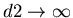 ,
so
,
so
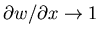 , and the number of call options to
own at the maturity time t* is 1. The value of the hedge equity
at t* is then
, and the number of call options to
own at the maturity time t* is 1. The value of the hedge equity
at t* is then
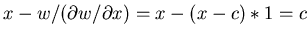 ,
as it should be.
,
as it should be.
Dennis Silverman
1999-05-20
![]() ), we calculate
), we calculate