


Next: Bibliography
Up: Solution of the Black
Previous: Post-Analysis
We show that the Green's function for the diffusion equation,
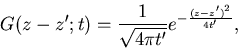 |
(35) |
satisfies the equation and behaves like a delta function at
t'=0.
Plugging the Green's function into the canonical diffusion equation,
Eq. 16, gives on both sides
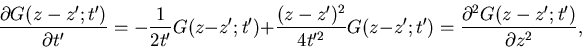 |
(36) |
verifying that it is a solution to the equation.
As 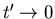 , for
, for 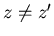 , the argument of the exponent goes
to
, the argument of the exponent goes
to 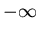 , and
, and
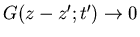 . For z=z', it goes to infinity
as
. For z=z', it goes to infinity
as
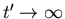 . The integral over z' can be found by
substituting
. The integral over z' can be found by
substituting
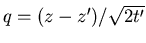 and gives
and gives
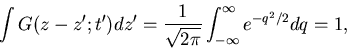 |
(37) |
showing that it is correctly normalized to be the solution for
a delta function source or point source at
z=z' when 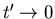 .
.



Next: Bibliography
Up: Solution of the Black
Previous: Post-Analysis
Dennis Silverman
1999-05-20
![]() , for
, for ![]() , the argument of the exponent goes
to
, the argument of the exponent goes
to ![]() , and
, and
![]() . For z=z', it goes to infinity
as
. For z=z', it goes to infinity
as
![]() . The integral over z' can be found by
substituting
. The integral over z' can be found by
substituting
![]() and gives
and gives