Wetting Near Triple Points

K. G. Sukhatme, J. E. Rutledge and P. Taborek,

Phys. Rev. Lett., V 80, p. 129 (Jan. 1998)

Introduction

Experimental Setup

Data

Discussion

Results

References

Discussion

Pandit and Fisher [10] pointed out that the stability of various surface phases depends critically on the relative size of the surface tensions s_lv, s_sw, s_sl, s_lw, and s_vw (where l=liquid, s=solid, v=vapor and w=wall), and that a large number of surface phase transitions are possible in the vicinity of the triple point. Pettersen Lysek, and Goodstein [14] have constructed a simple phenomenological model in which the film is regarded as a slab or slabs of bulk phase with the surface tension, van der Waals potentials and other effects treated as perturbations. We have used this type of model to interpret our data. The basis of the method is to write the grand free energy W(m,T;z), for a film of arbitrary thickness z and minimize W with respect to z. Near the triple point, there are three free energies W_l, W_s, and W_lay, for the liquid, solid and layered film which need to be considered; the stable phase is of course the one with the lowest value of W. For example, the free energy of the layered phase for arbitrary values of the thickness of the liquid and solid slabs z_l and z_s is:

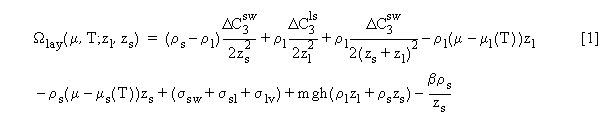
where r_i are the densities, m_i(T) are the bulk chemical potentials, and DC₃^ijare differences of van der Waals C₃ coefficients for the various bulk phases. 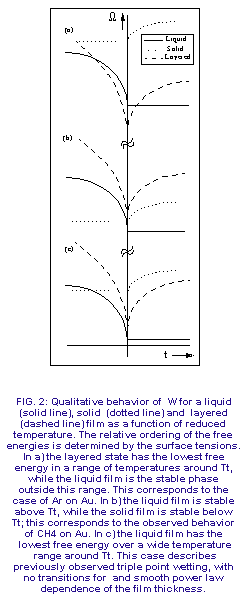The terms proportional to m-m_i(T) express the cost of forming a phase away from bulk coexistence. The term containing the surface tensions s_ij accounts for the energy required to form solid-wall, solid-liquid and liquid vapor interfaces. The term proportional to mgh accounts for the gravitational potential energy of the film, while the last term proportional to b accounts for the strain energy in the solid part of the film [1, 2]. Similar terms appear in W_s and W_l. See references [14,15] for further details.

Equation (1) and its analogues for W_s and W_l can be numerically minimized with respect to the z_i. The equilibrium W, the surface phase, and the film thicknesses are then determined by the lowest lying branch at each temperature. The relative positions of the three branches are determined by the magnitudes of the surface tensions. Figure 3 shows three different orderings of the free energies with m=the bulk coexistence value. The orderings correspond to different sequences of surface phase transitions near T_t. The qualitative behavior of each free energy branch is independent of the values of the parameters. The single phase branches have essentially constant values of W as long as the corresponding bulk phase is stable, with a cusp-like rise at the triple point where the bulk phase becomes metastable. W_lay is V-shaped with a sharp minimum at T_t. Figure 3a corresponds to the Ar surface phase diagram obtained from the data in Figure 1 with a high and low temperature liquid phase separated by a layered phase near T_t. Figure 3b shows a direct transition from liquid to solid at a temperature very close to T_t, which we believe is the case for CH₄. Figure 3c illustrates the triple point wetting scenario inferred from all previous experiments in which liquid films coexist with bulk solid over a wide range of temperature.