Abstract
Introduction
Experimental Setup
Data
Discussion
Results
References
|
 |
Results
 To compare the model
with the experiments, the zi given by the equilibrium W
can be compared to the data in Figures 1 and 2. This requires numerical
values for the parameters in the free energy of Eq. 1. Although the densities
[16], van der Waals coefficients [17], bulk chemical potentials, and slv
are known, ssl and the elastic strain
parameter b are not. To compare the model
with the experiments, the zi given by the equilibrium W
can be compared to the data in Figures 1 and 2. This requires numerical
values for the parameters in the free energy of Eq. 1. Although the densities
[16], van der Waals coefficients [17], bulk chemical potentials, and slv
are known, ssl and the elastic strain
parameter b are not. 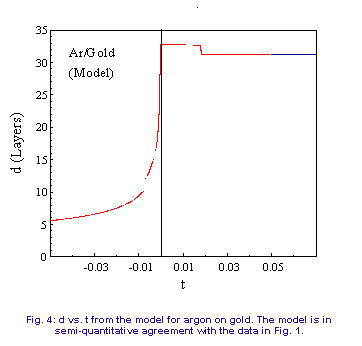 If
ssw, ssl
and b are treated as temperature independent
fitting parameters, we find that the model can not reproduce the features
we observe at t=-0.007 and 0.02. Both the elastic constants which determine
b and the surface tensions are in fact temperature dependent. If we include
a linear coefficient of temperature variation for ssl
and b as additional fitting parameters,
we obtain qualitative agreement between the model and the data. The parameters
resulting from the fitting procedure are physically reasonable. Details
will be given elsewhere [15]. Figure 4 shows the coverage as a function
of temperature for Ar on Au. The model accurately reproduces the positions
of the discontinuities. In the liquid phase, the model predicts that the
film thickness obeys a power law with an exponent of -0.34, and an exponent
of -0.27 in the layered phase, in reasonable agreement with the data. If
ssw, ssl
and b are treated as temperature independent
fitting parameters, we find that the model can not reproduce the features
we observe at t=-0.007 and 0.02. Both the elastic constants which determine
b and the surface tensions are in fact temperature dependent. If we include
a linear coefficient of temperature variation for ssl
and b as additional fitting parameters,
we obtain qualitative agreement between the model and the data. The parameters
resulting from the fitting procedure are physically reasonable. Details
will be given elsewhere [15]. Figure 4 shows the coverage as a function
of temperature for Ar on Au. The model accurately reproduces the positions
of the discontinuities. In the liquid phase, the model predicts that the
film thickness obeys a power law with an exponent of -0.34, and an exponent
of -0.27 in the layered phase, in reasonable agreement with the data.
 A similar analysis
of the CH4 data shows that the free energy diagrams for this
case look qualitatively like Figure 3b. The fact that the film thickness
is independent of temperature above Tt implies that the liquid
branch lies below both the solid and layered branch in this temperature
range. The smooth behavior of the thickness below Tt as well
as the non-divergent temperature dependence of the thickness suggests that
the film is entirely solid. As Fig 3b shows, the surface transition can
lie extremely close to Tt even for substantial offsets in the
W vs. t curves. In this scenario, the layered
state is never stable. This may be related to the fact that we observe
substantial hysteresis in the bulk phase transition. Without a layered
state, formation of the solid requires a nucleation event. For Ar, the
solid can grow continuously from the partially solid layered film. A similar analysis
of the CH4 data shows that the free energy diagrams for this
case look qualitatively like Figure 3b. The fact that the film thickness
is independent of temperature above Tt implies that the liquid
branch lies below both the solid and layered branch in this temperature
range. The smooth behavior of the thickness below Tt as well
as the non-divergent temperature dependence of the thickness suggests that
the film is entirely solid. As Fig 3b shows, the surface transition can
lie extremely close to Tt even for substantial offsets in the
W vs. t curves. In this scenario, the layered
state is never stable. This may be related to the fact that we observe
substantial hysteresis in the bulk phase transition. Without a layered
state, formation of the solid requires a nucleation event. For Ar, the
solid can grow continuously from the partially solid layered film.
 In summary, we have
documented two scenarios for triple point wetting which are distinctly
different from those previously reported. They are characterized by first
order surface phase transitions at temperatures close to but not coincident
with Tt and by temperature dependence of the coverage which
differs markedly from . The phase behavior of films near the triple point
depends critically on rather subtle variations in the surface tensions
and their temperature dependence. The thermodynamic model of Ref. [14]
provides a useful framework for analysis of these effects. In summary, we have
documented two scenarios for triple point wetting which are distinctly
different from those previously reported. They are characterized by first
order surface phase transitions at temperatures close to but not coincident
with Tt and by temperature dependence of the coverage which
differs markedly from . The phase behavior of films near the triple point
depends critically on rather subtle variations in the surface tensions
and their temperature dependence. The thermodynamic model of Ref. [14]
provides a useful framework for analysis of these effects.
 This work was supported
by NSF grant DMR 9623976. This work was supported
by NSF grant DMR 9623976.
|
|

