Abstract
Introduction
Experiment
Results
Discussion
References
Projects Page
|
 |
Experiment
 We have measured adsorption
isotherms using a quartz crystal microbalance [9,10]. The microbalances
were used at their third harmonic at a frequency of ~5.5 MHz, so that their
mass sensitivity was approximately 0.133 Hz/monolayer of liquid 3He.
The apparatus consisted of an OFHC copper vacuum can which contained two
microbalances. Cesium was evaporated from a source of pure elemental metal
onto both electrodes of one of the microbalances. The microbalance and
the vacuum can were maintained at a temperature less than ~6 K during the
evaporation to avoid contamination of the highly reactive cesium surface.
The second microbalance was left with bare gold electrodes. The purity
of the 3He used was >99.999%.
Measurements were conducted
on three different cesium substrates. The first was studied down to ~0.4
K using a recirculating 3He refrigerator for cooling, while
for the second and third surfaces the temperature range was extended by
installing a dilution refrigerator. In order to concentrate on the steepness
of the steps, most of the isotherms in the third set of data were not run
completely to saturation. Consequently, the steepness of the steps was
accurately measured but their location was not. The positions of the steps
measured in the first two data sets and in the completed isotherms of the
third data set are identical within the accuracy of the experiment. The
measured steepness of the steps (-df/dm) varied
by ~30% from one surface to the next, though in each case the temperature
dependence of the steepness was similar.
In order to asses the
effect of substrate inhomogeneity on the prewetting behavior, the substrates
were annealed. This was done by warming the cesium coated microbalance
to approximately 80 K for about 30 minutes. During annealing, the vacuum
can was again maintained at a temperature below ~6 K. Measurements were
made on the first substrate both before and after annealing, while the
second and third surfaces were annealed immediately after they were evaporated.
The experimental results
are presented as the shift of the resonant frequency of the microbalance,-Df
, as a function of the chemical potential of the 3He as shown
in Figs. 1-3. Because the saturated vapor pressure of 3He spanned
6 orders of magnitude over the temperature range of this experiment, a
variety of techniques were required to measure the chemical potential.
For temperatures above ~0.55 K a room temperature capacitance manometer
was used to determine the pressure. For temperatures between ~0.3 and ~0.6,
an in situ capacitance manometer was used. In these two cases Dmwas
calculated from the pressure using the usual ideal gas approximation, Dm=
m- m0=
T ln(P/P0). Here m0 and
P0 are the chemical potential and pressure at liquid-vapor coexistence,
respectively.
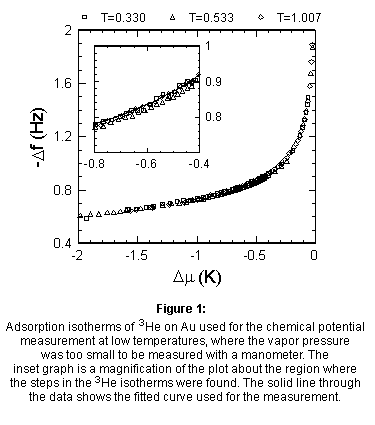
Below ~0.3 K the pressure
was too small to be accurately measured with the in situ manometer, so
a new technique had to be devised to measure Dm.
We found that the gold plated microbalance could be used as a chemical
potential meter. This technique relies on the observation that the frequency
shift of the gold plated microbalance is a function of only the chemical
potential offset, independent of temperature [11]. This behavior can be
seen in Fig. 1 which shows the frequency shift of the gold plated microbalance
plotted vs. Dm for three different temperatures,
T = 0.330 K, T = 0.533 K, and T = 1.007 K. A fit of the isotherm at T =
0.330 K was used to convert the measured frequency shifts of the gold-plated
microbalance to chemical potentials. The inset graph of Fig. 1 shows the
data and the fit curve for chemical potential offsets near the location
of the steps found in the 3He adsorption isotherms. The ~10
mHz shift between the 0.533 K data and the other two data sets provides
an estimate for the error in this measurement method, which in this case
leads to a systematic error of ±0.02 K in the chemical potential. The
typical noise in our frequency measurements is ±5 mHz. As a result the
random error in our determination of Dm is ±0.01
K.
|
|
