| Abstract
Introduction
Experimental
Methods
Data
Discussion
Conlcusions
References
Projects Page
|
 |
Data
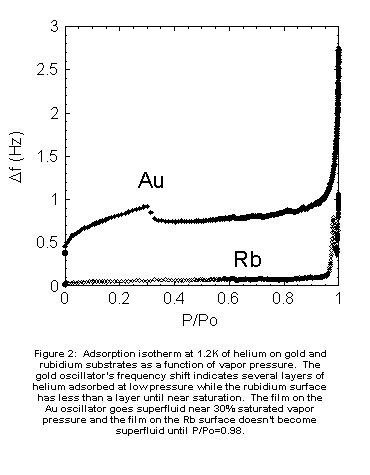  In
order to cover a large region of the m-T plane,
isotherms were performed from T=0.15K to 2.2K in the pressure range from
vacuum to liquid-vapor coexistence. Figure 2 shows a frequency shift isotherm
at 1.2K for both the Au and the Rb-coated oscillators. Note that the Au
oscillator has a frequency shift corresponding to several adsorbed layers
even at very low pressures, while the Rb oscillator shows less than one
half monolayer adsorption until quite near the saturated vapor pressure.
In subsequent figures, we will usually omit the low coverage, low pressure
regime and concentrate on the region near coexistence where the film thickness
changes rapidly. In Figure 3 we present a sample pair of isotherms
performed at 1.50K on surface 2. The figure shows the resonant frequency
shift, Df, and dissipation change, DR,
as a function of Dm. The system started in vacuum
and gas was slowly added to the experiment cell. This type of isotherm
in which Dm increases as a function of
time is referred to as a “forward” isotherm and is indicated by the open
diamonds in Figure 3. At low chemical potential Fig. 3a indicates
that at most only 0.2 monolayers are adsorbed. Near Dm
= -0.05 K, Df abruptly increases. This behavior is characteristic of a
prewetting thick/thin transition. When the frequency shift reaches a value
of 0.8 Hz (corresponding to a thickness of 4 layers), the film undergoes
a superfluid transition. This transition is identified by two significant
features: Df drops as the superfluid fraction
uncouples from the oscillator and DR has the
predicted dynamic KT peak at the same Dm (Figure
3b). As more helium is added to the cell, Df
continues to increase because the film thickness is rapidly increasing
and the oscillator has some non-transverse motion which couples to the
superfluid film. Since the film ends up in a thick state at saturation,
it is said to wet the rubidium. In
order to cover a large region of the m-T plane,
isotherms were performed from T=0.15K to 2.2K in the pressure range from
vacuum to liquid-vapor coexistence. Figure 2 shows a frequency shift isotherm
at 1.2K for both the Au and the Rb-coated oscillators. Note that the Au
oscillator has a frequency shift corresponding to several adsorbed layers
even at very low pressures, while the Rb oscillator shows less than one
half monolayer adsorption until quite near the saturated vapor pressure.
In subsequent figures, we will usually omit the low coverage, low pressure
regime and concentrate on the region near coexistence where the film thickness
changes rapidly. In Figure 3 we present a sample pair of isotherms
performed at 1.50K on surface 2. The figure shows the resonant frequency
shift, Df, and dissipation change, DR,
as a function of Dm. The system started in vacuum
and gas was slowly added to the experiment cell. This type of isotherm
in which Dm increases as a function of
time is referred to as a “forward” isotherm and is indicated by the open
diamonds in Figure 3. At low chemical potential Fig. 3a indicates
that at most only 0.2 monolayers are adsorbed. Near Dm
= -0.05 K, Df abruptly increases. This behavior is characteristic of a
prewetting thick/thin transition. When the frequency shift reaches a value
of 0.8 Hz (corresponding to a thickness of 4 layers), the film undergoes
a superfluid transition. This transition is identified by two significant
features: Df drops as the superfluid fraction
uncouples from the oscillator and DR has the
predicted dynamic KT peak at the same Dm (Figure
3b). As more helium is added to the cell, Df
continues to increase because the film thickness is rapidly increasing
and the oscillator has some non-transverse motion which couples to the
superfluid film. Since the film ends up in a thick state at saturation,
it is said to wet the rubidium.
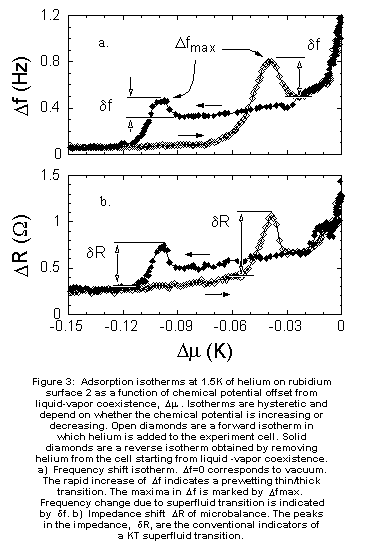  We
have systematically looked for hysteresis in the thin normal -> thick superfluid
transition by measuring “reverse” isotherms in which small amounts of helium
gas are sequentially removed from the experiment cell. In Figure 3, the
reverse isotherm, denoted by solid diamonds, starts at coexistence in the
thick superfluid state and is coincident with the forward isotherm down
to Dm = -0.03 K, where the two sets of data
diverge. On the reverse isotherm, the film remains superfluid until Dm
= -0.10 K, where the film first becomes normal (Df
and DR increase) and then goes through the prewetting
transition to the thin state. We
have systematically looked for hysteresis in the thin normal -> thick superfluid
transition by measuring “reverse” isotherms in which small amounts of helium
gas are sequentially removed from the experiment cell. In Figure 3, the
reverse isotherm, denoted by solid diamonds, starts at coexistence in the
thick superfluid state and is coincident with the forward isotherm down
to Dm = -0.03 K, where the two sets of data
diverge. On the reverse isotherm, the film remains superfluid until Dm
= -0.10 K, where the film first becomes normal (Df
and DR increase) and then goes through the prewetting
transition to the thin state.
 The data shown in
Fig 3 are typical of our data between 0.75 K and 1.95 K. Throughout this
range the forward and reverse Dm values at prewetting
and superfluid onset are strongly hysteretic. In addition, the superfluid
onset thicknesses, the onset superfluid jumps, and the dissipation peak
heights and areas are larger on the forward branch at each temperature.
At 1.95 K the hysteresis abruptly decreases and the forward and reverse
isotherms become nearly identical. Below 1.95 K the difference between
the prewetting and superfluid onset Dm values
is small and roughly temperature independent. Above 1.95 K the Dm
difference rapidly grows, and prewetting and superfluid onset become clearly
distinguishable transitions. The data shown in
Fig 3 are typical of our data between 0.75 K and 1.95 K. Throughout this
range the forward and reverse Dm values at prewetting
and superfluid onset are strongly hysteretic. In addition, the superfluid
onset thicknesses, the onset superfluid jumps, and the dissipation peak
heights and areas are larger on the forward branch at each temperature.
At 1.95 K the hysteresis abruptly decreases and the forward and reverse
isotherms become nearly identical. Below 1.95 K the difference between
the prewetting and superfluid onset Dm values
is small and roughly temperature independent. Above 1.95 K the Dm
difference rapidly grows, and prewetting and superfluid onset become clearly
distinguishable transitions.
 Isotherms from three
rubidium substrates in the temperature range 0.15K to 2.2K were used to
construct a Dm - T phase diagram shown in Figure
4. An open triangle marks the value of Dm at
the steepest point on the prewetting step and an open circle marks the
position of the dissipation peak on the forward isotherm at each temperature.
Corresponding solid symbols mark these features on the reverse isotherms.
Some of the scatter in the points in Figure 4 is due to variations among
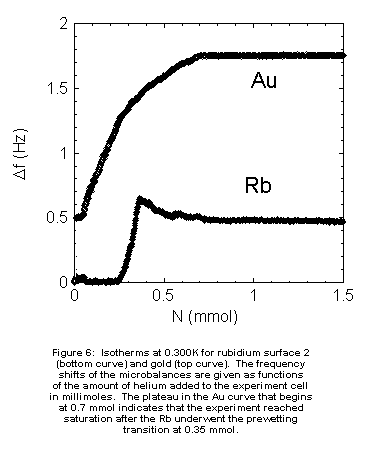
the 3 Rb surfaces; typical behavior of forward isotherms at T=1.22 K for
each of the 3 surfaces is shown in Figure 5. Note that the peak occurs
at approximately the same value of Dm for each
surface, but the size and shape of the peak varies from surface to surface. Isotherms from three
rubidium substrates in the temperature range 0.15K to 2.2K were used to
construct a Dm - T phase diagram shown in Figure
4. An open triangle marks the value of Dm at
the steepest point on the prewetting step and an open circle marks the
position of the dissipation peak on the forward isotherm at each temperature.
Corresponding solid symbols mark these features on the reverse isotherms.
Some of the scatter in the points in Figure 4 is due to variations among
the 3 Rb surfaces; typical behavior of forward isotherms at T=1.22 K for
each of the 3 surfaces is shown in Figure 5. Note that the peak occurs
at approximately the same value of Dm for each
surface, but the size and shape of the peak varies from surface to surface.
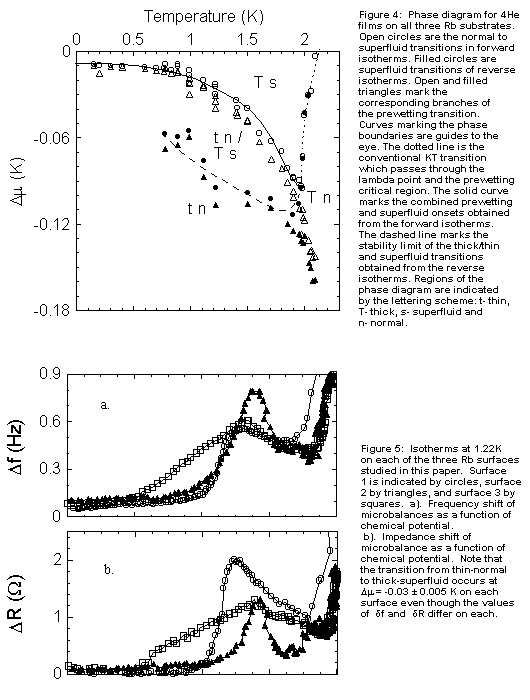
  The
solid line in Figure 4 connects the thin->thick transitions of the forward
isotherms and will be referred to as the prewetting line. Notice that it
does not intersect the liquid-vapor saturation line, Dm
= 0, implying that helium wets our rubidium surfaces at all temperatures.
This conclusion does not depend on subtleties of our method of measuring
Dm at low temperature. After prewetting and
superfluid onset, more gas must be added to the cell to reach saturation
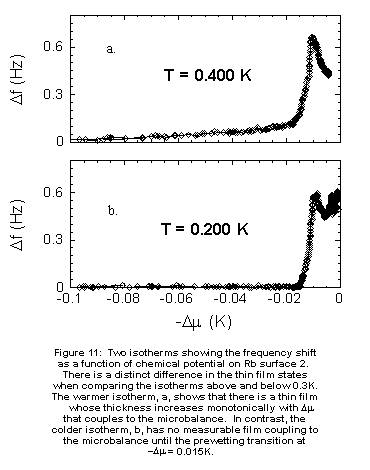
even at the lowest temperatures. This can clearly be seen in Figure 6,
which shows a plot of Df as a function of the
amount of gas admitted to the cell, N, for both the rubidium coated oscillator
and the bare gold oscillator at T=0.3K. The plateau in Df
vs. N for the gold oscillator indicates a region of bulk liquid-vapor coexistence
in which the adsorbed film has reached its asymptotic gravitationally limited
thickness. The prewetting peak on the Rb oscillator occurs at substantially
lower N than the coexistence value. The
solid line in Figure 4 connects the thin->thick transitions of the forward
isotherms and will be referred to as the prewetting line. Notice that it
does not intersect the liquid-vapor saturation line, Dm
= 0, implying that helium wets our rubidium surfaces at all temperatures.
This conclusion does not depend on subtleties of our method of measuring
Dm at low temperature. After prewetting and
superfluid onset, more gas must be added to the cell to reach saturation
even at the lowest temperatures. This can clearly be seen in Figure 6,
which shows a plot of Df as a function of the
amount of gas admitted to the cell, N, for both the rubidium coated oscillator
and the bare gold oscillator at T=0.3K. The plateau in Df
vs. N for the gold oscillator indicates a region of bulk liquid-vapor coexistence
in which the adsorbed film has reached its asymptotic gravitationally limited
thickness. The prewetting peak on the Rb oscillator occurs at substantially
lower N than the coexistence value.
 It is interesting
to inquire whether the Kosterlitz-Thouless picture, which successfully
describes superfluid onset on both conventional substrates and Cs, can
also account for the combined superfluid/prewetting transition we observe
on Rb. We find that although the basic features of a superfluid jump and
enhanced dissipation clearly exist, the universal KT predictions do not
apply to superfluid onset on Rb. Although the Kosterlitz-Thouless theory
makes no explicit prediction about the absolute thickness of the film at
superfluid onset, the jump in the superfluid fraction ss depends only on
T and universal constants. [2] : It is interesting
to inquire whether the Kosterlitz-Thouless picture, which successfully
describes superfluid onset on both conventional substrates and Cs, can
also account for the combined superfluid/prewetting transition we observe
on Rb. We find that although the basic features of a superfluid jump and
enhanced dissipation clearly exist, the universal KT predictions do not
apply to superfluid onset on Rb. Although the Kosterlitz-Thouless theory
makes no explicit prediction about the absolute thickness of the film at
superfluid onset, the jump in the superfluid fraction ss depends only on
T and universal constants. [2] :
|
sS(TC)
= 8 p m kB TC /
h2 |
(2) |
where m is the mass of a helium atom, kB is Boltzmann’s constant,
TC is the transition temperature and sS
is the coverage in atoms/m2. In terms of our experimental observables,
this implies that the frequency shift at onset df
is numerically given by
|
df = -4 fn2
m sS(TC)
/ n Rq
=0.1584 Hz / K × TC |
(3) |
where fn is the resonant frequency of the nth harmonic and Rq
is the transverse acoustic impedance of quartz (Rq~ 8.862 ×
106 kg/m2sec). This prediction is manifestly independent
of the substrate. Furthermore, since the KT transition is a higher order
transition, it cannot be superheated or supercooled, so no hysteresis in
the onset temperature is expected.
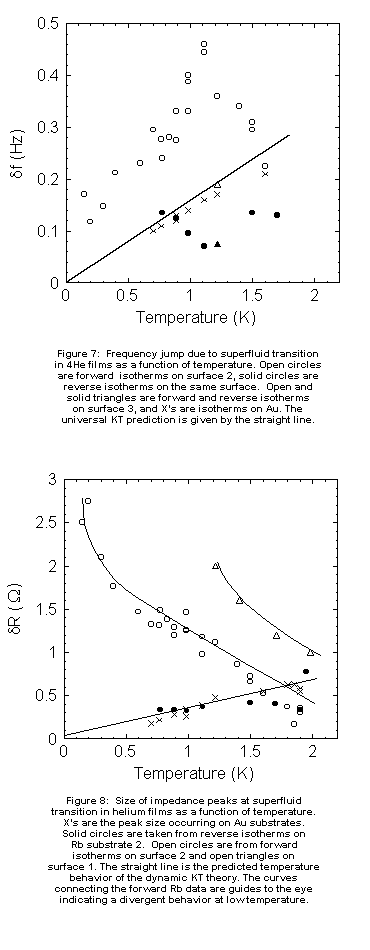  In
our isotherms, the abrupt step in Df on the
thick film side of the prewetting transition, denoted by df
in Figure 3, can be attributed to a KT-like jump in the superfluid density.
df does not, however, obey the KT prediction
of Eq. 2. For example, the data at 1.50K (Figure 3) shows a
superfluid jump of 0.35 Hz (1.4 layers) on the forward isotherm, while
the reverse isotherm shows a jump of 0.18 Hz (0.7 layers). The fact that
these two values are different is a violation of the KT prediction that
the size of the jump is a unique function of T. Furthermore, neither of
them is equal to the predicted value of 0.25 Hz (1.0 layer). A number of
isotherms like Figure 3 have been used to construct a plot of the magnitude
of the superfluid jump at onset, df, as a function
of T for both forward and reverse branches on Rb for surfaces 2 & 3,
as shown in Figure 7. The universal KT prediction (straight line from Eq.
2) and the df vs. T results from the gold oscillator,
determined by the same method we used on the Rb oscillator, are shown for
comparison. The agreement between the gold data and the KT prediction is
typical of all previously studied surfaces [9,16,18, 25], and provides
a check of our experimental procedure. In
our isotherms, the abrupt step in Df on the
thick film side of the prewetting transition, denoted by df
in Figure 3, can be attributed to a KT-like jump in the superfluid density.
df does not, however, obey the KT prediction
of Eq. 2. For example, the data at 1.50K (Figure 3) shows a
superfluid jump of 0.35 Hz (1.4 layers) on the forward isotherm, while
the reverse isotherm shows a jump of 0.18 Hz (0.7 layers). The fact that
these two values are different is a violation of the KT prediction that
the size of the jump is a unique function of T. Furthermore, neither of
them is equal to the predicted value of 0.25 Hz (1.0 layer). A number of
isotherms like Figure 3 have been used to construct a plot of the magnitude
of the superfluid jump at onset, df, as a function
of T for both forward and reverse branches on Rb for surfaces 2 & 3,
as shown in Figure 7. The universal KT prediction (straight line from Eq.
2) and the df vs. T results from the gold oscillator,
determined by the same method we used on the Rb oscillator, are shown for
comparison. The agreement between the gold data and the KT prediction is
typical of all previously studied surfaces [9,16,18, 25], and provides
a check of our experimental procedure.
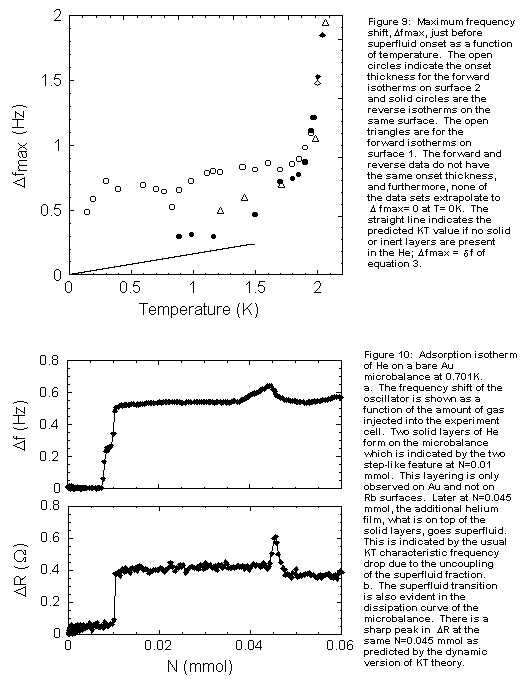
 The temperature dependence
of the dissipation peak associated with superfluid onset on Rb is also
anomalous. The forward and reverse dR measurements
on Rb for surfaces 1 and 2 and the dR values
on Au are shown in Figure 8. The dynamic KT prediction for the dissipation,
although not universal, is proportional to T [3]; the expected straight
line behavior is also shown in Figure 8. The reverse Rb dissipation peaks
and the peaks on Au are similar and conform with the KT picture. However,
the forward isotherm dR values grow rapidly
with decreasing temperature and in fact appear to be diverging as T goes
toward 0 K. Although the absolute value of the loss is different for the
two surfaces, the trend of increasing loss with decreasing temperature
is seen on both. The temperature dependence
of the dissipation peak associated with superfluid onset on Rb is also
anomalous. The forward and reverse dR measurements
on Rb for surfaces 1 and 2 and the dR values
on Au are shown in Figure 8. The dynamic KT prediction for the dissipation,
although not universal, is proportional to T [3]; the expected straight
line behavior is also shown in Figure 8. The reverse Rb dissipation peaks
and the peaks on Au are similar and conform with the KT picture. However,
the forward isotherm dR values grow rapidly
with decreasing temperature and in fact appear to be diverging as T goes
toward 0 K. Although the absolute value of the loss is different for the
two surfaces, the trend of increasing loss with decreasing temperature
is seen on both.
 On a conventional
substrate, the minimum helium coverage required for superfluidity is considerably
higher than the KT critical coverage defined in Eq. 2. This phenomenon
is attributed to the existence of a solid-like “dead layer” which is immobilized
by the substrate potential. This layer is typically about two monolayers
thick, but on weak substrates such as solid hydrogen, the critical coverage
for superfluidity at T=0 is approximately 1/2 layer [26-28]. Rb, which
is even weaker than H2, is expected to have a very low critical
coverage at low temperature. In contrast to this expectation, our data
seem to indicate that more than two layers of 4He can remain
in the normal state on Rb even at T=0. On a conventional
substrate, the minimum helium coverage required for superfluidity is considerably
higher than the KT critical coverage defined in Eq. 2. This phenomenon
is attributed to the existence of a solid-like “dead layer” which is immobilized
by the substrate potential. This layer is typically about two monolayers
thick, but on weak substrates such as solid hydrogen, the critical coverage
for superfluidity at T=0 is approximately 1/2 layer [26-28]. Rb, which
is even weaker than H2, is expected to have a very low critical
coverage at low temperature. In contrast to this expectation, our data
seem to indicate that more than two layers of 4He can remain
in the normal state on Rb even at T=0.
 The maximum frequency
shift Dfmax associated with the prewetting
steps shown in Figure 3 is a convenient measure of the normal coverage
at superfluid onset. Figure 9 shows a plot of Dfmax
for both forward and reverse isotherms as a function of temperature for
surfaces 1 and 3. The solid straight line shows the expected value of df
from the KT theory Eq. 3 which is equal to Dfmax
if there is no dead layer. Like all of the other features of the isotherms,
Dfmax is hysteretic. On the reverse
isotherms, Dfmax seems to approach
the KT line at the lowest accessible temperatures. On the forward isotherms,
Dfmax has almost the same temperature
dependence as the KT prediction, but it extrapolates to a remarkably high
value of 2.0 layers at T=0. This can be compared to the typical onset behavior
on gold, illustrated in Figure 10, which shows two steps corresponding
to the formation of 2 (presumably solid) layers followed by superfluid
onset at essentially the same value of Dfmax
we observe on Rb. The maximum frequency
shift Dfmax associated with the prewetting
steps shown in Figure 3 is a convenient measure of the normal coverage
at superfluid onset. Figure 9 shows a plot of Dfmax
for both forward and reverse isotherms as a function of temperature for
surfaces 1 and 3. The solid straight line shows the expected value of df
from the KT theory Eq. 3 which is equal to Dfmax
if there is no dead layer. Like all of the other features of the isotherms,
Dfmax is hysteretic. On the reverse
isotherms, Dfmax seems to approach
the KT line at the lowest accessible temperatures. On the forward isotherms,
Dfmax has almost the same temperature
dependence as the KT prediction, but it extrapolates to a remarkably high
value of 2.0 layers at T=0. This can be compared to the typical onset behavior
on gold, illustrated in Figure 10, which shows two steps corresponding
to the formation of 2 (presumably solid) layers followed by superfluid
onset at essentially the same value of Dfmax
we observe on Rb.
  Discussion
thus far has focussed on the thin to thick transitions, but there also
appears to be a qualitative change in behavior of the thin film phase which
occurs near 0.3K and may conceivably be related to the transition reported
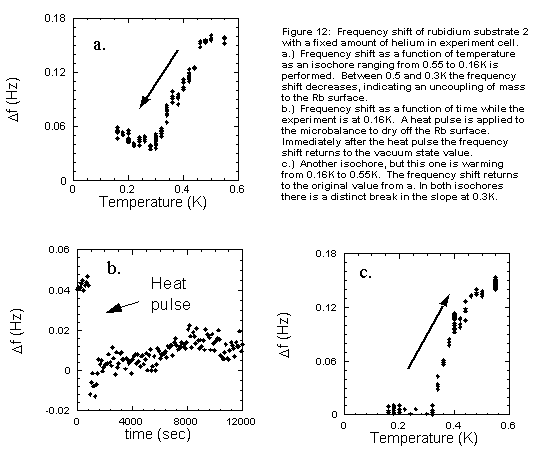
by Wyatt et al. [13]. Figure 11 shows the frequency shift for
two isotherms at 0.2K and 0.4K for surface 2. Both isotherms show a prewetting
step and superfluid onset, but the thin phase (Dm<-0.017K)
is quite different in the two cases. The 0.2K isotherm shows
no shift in the frequency from the vacuum value until the prewetting step,
while the 0.4K isotherm has a continuously increasing value of Df
and a frequency shift of 0.2 Hz (corresponding to 0.8 layer) at the beginning
of the prewetting transition. One possible explanation of this behavior
is a superfluid [13] or other type of phase transition in the thin phase.
Another possibility is that the observed differences are due to the fact
that the saturated vapor pressure varies by more than a factor of 107
between 0.2K and 0.4K, resulting in significantly different equilibrium
times. To test the possible role of mass transfer kinetics, we measured
isochores with both increasing and decreasing temperatures.
We began with a vacuum at 0.55K and added just enough helium to the cell
to increase the chemical potential to a value below the prewetting transition
so the adsorbed film would still be in a thin phase. The experiment was
then cooled down to 0.2K with this fixed amount of helium in the experiment
(Figure 12a). As the experiment cooled, the frequency shift decreased indicating
that the coupled mass to the microbalance was changing. This could either
be due to helium leaving the microbalance or a transition to a thin superfluid
film; it cannot be attributed to a mass transfer bottleneck, since the
normal film was present at high temperature. The film could be removed
from the oscillator by applying a heat pulse to the microbalance at 0.2K,
as shown in Figure 12b. The frequency shift remained close to zero for
several hours after the heat pulse. The temperature of the experiment was
subsequently increased to 0.55K and the microbalance frequency returned
to its initial value as shown in Figure 12c. In both the heating and cooling
cycles, 0.3K marks a change in slope of Df. Discussion
thus far has focussed on the thin to thick transitions, but there also
appears to be a qualitative change in behavior of the thin film phase which
occurs near 0.3K and may conceivably be related to the transition reported
by Wyatt et al. [13]. Figure 11 shows the frequency shift for
two isotherms at 0.2K and 0.4K for surface 2. Both isotherms show a prewetting
step and superfluid onset, but the thin phase (Dm<-0.017K)
is quite different in the two cases. The 0.2K isotherm shows
no shift in the frequency from the vacuum value until the prewetting step,
while the 0.4K isotherm has a continuously increasing value of Df
and a frequency shift of 0.2 Hz (corresponding to 0.8 layer) at the beginning
of the prewetting transition. One possible explanation of this behavior
is a superfluid [13] or other type of phase transition in the thin phase.
Another possibility is that the observed differences are due to the fact
that the saturated vapor pressure varies by more than a factor of 107
between 0.2K and 0.4K, resulting in significantly different equilibrium
times. To test the possible role of mass transfer kinetics, we measured
isochores with both increasing and decreasing temperatures.
We began with a vacuum at 0.55K and added just enough helium to the cell
to increase the chemical potential to a value below the prewetting transition
so the adsorbed film would still be in a thin phase. The experiment was
then cooled down to 0.2K with this fixed amount of helium in the experiment
(Figure 12a). As the experiment cooled, the frequency shift decreased indicating
that the coupled mass to the microbalance was changing. This could either
be due to helium leaving the microbalance or a transition to a thin superfluid
film; it cannot be attributed to a mass transfer bottleneck, since the
normal film was present at high temperature. The film could be removed
from the oscillator by applying a heat pulse to the microbalance at 0.2K,
as shown in Figure 12b. The frequency shift remained close to zero for
several hours after the heat pulse. The temperature of the experiment was
subsequently increased to 0.55K and the microbalance frequency returned
to its initial value as shown in Figure 12c. In both the heating and cooling
cycles, 0.3K marks a change in slope of Df.
|
|







