Superfluid Onset and Prewetting of 4He on Rubidium

J. A. Phillips, D. Ross, P. Taborek and J. E. Rutledge 
Department of Physics and Astronomy 
University of California, Irvine 92697 

(1998)
 
 
Abstract 

Introduction 

Experimental Methods 

Data 

Discussion 

Conlcusions 

References 
 
 
 
 

Projects Page 
 
 
 
 

Experimental Methods

The response of high Q mechanical oscillators to an adsorbed helium film has been an important probe of both prewetting and superfluid onset [4, 5, 8, 9, 16-22].   The experiments reported here utilize AT cut quartz oscillators as microbalances. The microbalances consist of a quartz substrate shaped like a thin convex lens about 1 cm in diameter and 0.1 cm thick. A gold electrode covers the center of each side and defines the mass sensitive area. When a voltage is applied to the electrodes, opposite faces of the crystal move transversely to the thickness of the device at a third harmonic of 5.5 MHz. Since the quartz microbalances oscillate in a shear mode, in a first approximation only the viscously clamped normal fraction of the helium film, including any solid layers that may be present, will couple to the substrate. When the film undergoes the normal to superfluid transition, one sees a sharp step in the resonant frequency because of the decoupling of the zero viscosity superfluid film from the substrate. Another signature of the superfluid transition in helium films is a peak in the dissipation (1/Q). A quantitative understanding of these effects is based on a finite frequency modification of static KT theory [3]. 
In an electrical circuit, a quartz microbalance is equivalent to a damped series LC resonant circuit with a resonant frequency, f, and real part of the impedance, R. Adsorbed films shift the resonant frequency from the vacuum value by an amount proportional to the film mass, Df. Losses in the film shift the real part of the impedance by DR. If the crystals were planar and infinite in diameter, their motion would be strictly transverse with opposite faces moving parallel to themselves. In real devices the resonant modes necessarily contains a small admixture of motion perpendicular to the faces [23]. This means that even at low temperatures where the superfluid fraction is virtually 1, the devices retain some sensitivity to variations in the adsorbed mass. Depending on the oscillator, 10 - 20% of the superfluid couples to the microbalance. This provides a detection sensitivity of 0.025 - 0.05 Hz/layer of superfluid compared with a sensitivity of 0.25 Hz/layer of normal liquid 4He.
Rubidium adsorption surfaces are prepared by evaporating vacuum distilled rubidium metal over the gold electrodes of a microbalance. During evaporation and subsequent annealing, the substrate and experimental cell are maintained below 6 K to ensure ultra-high vacuum conditions. The data reported here were obtained on three different Rb surfaces. Surfaces 1 and 3 had 75 layers of Rb evaporated on each side of the microbalance and were then annealed near 80K for half an hour. Surface 2 was prepared in two stages, each of which consisted of evaporating 38 layers per side and annealing at 80K for half an hour. 
The cell is cooled by a dilution refrigerator and connected through a capillary to a source of high purity helium gas. It is also connected to a pumping system through a much larger tube and a cold valve. This configuration allows us to add 4He to the cell at any temperature and to remove it above 0.7 K. At lower temperatures the removal rate is prohibitively low.
Our raw data consist of adsorption isotherms measured at temperatures between 0.15 K and 2.2 K.  They are presented as plots of Df and DR as functions of the pressure or the chemical potential offset from saturation, Dm.  Depending on the vapor pressure, the chemical potential is determined in one of three ways.  Above 1.2 K the pressure is measured by a room temperature capacitive manometer.  Between 0.8 K and 1.2 K the pressure is measured by an in situ capacitance gauge calibrated against the room temperature manometer.  In these cases Dm was calculated from the pressure using the ideal gas approximation, Dm = m - m0 = T ln(P / P0).  Here m0 and P0 are the chemical potential and pressure at liquid-vapor coexistence, respectively.  When an isotherm is performed below 0.8K, the vapor pressure is too low to be measured by either one of the pressure gauges and another method must be used.
For the low temperature isotherms we make use of a second microbalance in the experiment cell which has standard gold electrodes. On this strong substrate, it is plausible that the coverage (or equivalently Df) is a function of only  Dm, and not of T and P separately. This conjecture has been experimentally verified for 3He and used for low temperature chemical potential measurements in a previous study [24]. The application of the technique for 4He is complicated by the fact that the superfluid fraction of the adsorbed film is temperature dependent and the sensitivities of the microbalance to superfluid and normal fluid are different. Because of this difference, Df is not simply proportional to the coverage, and plots of Df as a function of Dm for various temperatures yield a family of distinct curves. It is possible, however, to collapse this family of curves onto a single universal curve by making a suitable correction for the sensitivity of the microbalance to the superfluid. 
The sensitivity to the superfluid is obtained by measuring several isotherms at  high enough temperatures that the previously mentioned pressure gauges can be used to determine the chemical potential. The isotherms can be normalized by considering the frequency shift Dfn that would be measured if the film had the same thickness but was entirely normal fluid. Dfn is related to the measured value Df by:
 
 
Dfn = Df / (rN/r + k rS/r) (1)
 

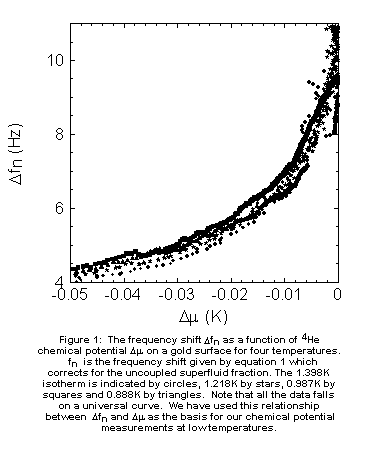
figure 1where rN/r and rS/r are the temperature dependent normal and superfluid ratios respectively and k is the fraction of superfluid that couples to the oscillator. For a suitably chosen value of k (in our case k=0.20) isotherms taken over a wide range of temperature fall on a single curve when Dfn is plotted as a function of Dm, as shown in Figure 1. Similar values of the superfluid coupling factor where obtained in previous experiments on mylar torsional oscillators [4, 5], while much larger values are observed on exfoliated graphite [21]. We assume that the functional dependence of  Dfn on Dm does not change between 0.8 K and 0.15 K. A line of best fit is drawn through the data to give the function needed to convert the gold oscillator’s frequency shift to chemical potential at low temperatures (below 0.8K). The uncertainty in Dm in this method is approximately 5mK.