| Abstract
Introduction
Experimental
Methods
Data
Discussion
Conlcusions
References
Projects Page
|
 |
Discussion
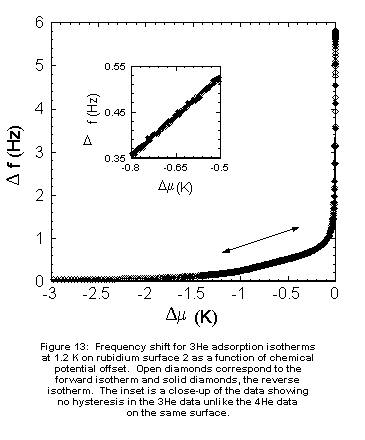  The
most striking feature of the phase diagram in Figure 4 is the hysteresis
in the prewetting thick/thin transition. Prewetting steps on Cs prepared
in a similar way as the Rb surfaces described here are essentially identical
in the forward and reverse directions [8]. On rough or porous surfaces,
however, capillary condensation can give rise to hysteretic behavior on
Cs [29]. We have ruled out this possibility on our substrates by carefully
measuring isotherms using 3He (for which neither wetting nor
superfluidity is an issue) on substrate 2; there was no observable hysteresis
and no excessive adsorption at saturation (Figure 13), suggesting that
the hysteresis we observe with 4He is an intrinsic property
of the 4He surface phases, and not an artifact due to the substrate.
Qualitatively similar hysteresis was observed on our surface 1. Demolder
et al. [11] used a heat flow technique to map the superfluid onset of 4He
on Rb at temperatures between 1.0 K and 1.7 K. They also found that its
position in the m - T plane was hysteretic.
Our measurements of the Dm at onset for forward
isotherms agree with their forward isotherms in the region where our data
overlap. The width of the hysteresis in Dm which
they observe is considerably narrower than ours, possibly because their
helium films are carrying a finite heat current. The
most striking feature of the phase diagram in Figure 4 is the hysteresis
in the prewetting thick/thin transition. Prewetting steps on Cs prepared
in a similar way as the Rb surfaces described here are essentially identical
in the forward and reverse directions [8]. On rough or porous surfaces,
however, capillary condensation can give rise to hysteretic behavior on
Cs [29]. We have ruled out this possibility on our substrates by carefully
measuring isotherms using 3He (for which neither wetting nor
superfluidity is an issue) on substrate 2; there was no observable hysteresis
and no excessive adsorption at saturation (Figure 13), suggesting that
the hysteresis we observe with 4He is an intrinsic property
of the 4He surface phases, and not an artifact due to the substrate.
Qualitatively similar hysteresis was observed on our surface 1. Demolder
et al. [11] used a heat flow technique to map the superfluid onset of 4He
on Rb at temperatures between 1.0 K and 1.7 K. They also found that its
position in the m - T plane was hysteretic.
Our measurements of the Dm at onset for forward
isotherms agree with their forward isotherms in the region where our data
overlap. The width of the hysteresis in Dm which
they observe is considerably narrower than ours, possibly because their
helium films are carrying a finite heat current.
 Another significant
difference between Rb and Cs is the width of the prewetting steps which
are approximately 3 times wider on Rb than Cs. Below the prewetting critical
temperature, Tcpw, prewetting is a first order transition
which ideally occurs at constant chemical potential, but even for T>Tcpw,
maxima in the compressibility of the supercritical film give rise to broader
step-like structures in isotherms. Monitoring the temperature dependence
of the width of the transition is a standard method of locating the prewetting
critical point [8]. In contrast to the Cs case, the width of the prewetting
transitions on Rb is a smooth, almost linear function of temperature, with
no obvious break in slope. These observations suggest that our Rb surfaces
are more disordered than our Cs surfaces. The source of the substrate
inhomogeneity is presumably variations in the wetting properties of substrate
patches with different crystallographic orientation [30]. If this is the
case, then the observed hysteresis is associated with prewetting broadened
by the effects of substrate inhomogeneity. In this interpretation, the
reverse branch is due to a spinodal line (stability limit) of the thick
film superfluid phase. Our belief that the forward branch represents the
equilibrium transition while the reverse branch is metastable is based
on the fact that the Rb substrate is surrounded by strong binding surfaces
(quartz and gold) which are covered with a thick superfluid film whenever
the helium film on the Rb undergoes a thick/thin transition on either the
forward or reverse isotherm. The thin->thick transition on the forward
isotherm is nucleated at the edge of the Rb, while the thick->thin transition
on the reverse isotherm requires a fluctuation and can therefor be supercooled.
The reduction of hysteresis in the region near 1.95 K marks the remnant
of the broadened prewetting critical point. Above 1.95K, there is some
remaining hysteresis in the prewetting transitions, but not in the position
of the KT line. Prewetting is in the 2D Ising universality class, and the
phase transitions in this type of system are well known to be strongly
affected by disorder [31-34], while the KT transition, which is in the
XY universality class, is relatively insensitive to disorder [35]. Another significant
difference between Rb and Cs is the width of the prewetting steps which
are approximately 3 times wider on Rb than Cs. Below the prewetting critical
temperature, Tcpw, prewetting is a first order transition
which ideally occurs at constant chemical potential, but even for T>Tcpw,
maxima in the compressibility of the supercritical film give rise to broader
step-like structures in isotherms. Monitoring the temperature dependence
of the width of the transition is a standard method of locating the prewetting
critical point [8]. In contrast to the Cs case, the width of the prewetting
transitions on Rb is a smooth, almost linear function of temperature, with
no obvious break in slope. These observations suggest that our Rb surfaces
are more disordered than our Cs surfaces. The source of the substrate
inhomogeneity is presumably variations in the wetting properties of substrate
patches with different crystallographic orientation [30]. If this is the
case, then the observed hysteresis is associated with prewetting broadened
by the effects of substrate inhomogeneity. In this interpretation, the
reverse branch is due to a spinodal line (stability limit) of the thick
film superfluid phase. Our belief that the forward branch represents the
equilibrium transition while the reverse branch is metastable is based
on the fact that the Rb substrate is surrounded by strong binding surfaces
(quartz and gold) which are covered with a thick superfluid film whenever
the helium film on the Rb undergoes a thick/thin transition on either the
forward or reverse isotherm. The thin->thick transition on the forward
isotherm is nucleated at the edge of the Rb, while the thick->thin transition
on the reverse isotherm requires a fluctuation and can therefor be supercooled.
The reduction of hysteresis in the region near 1.95 K marks the remnant
of the broadened prewetting critical point. Above 1.95K, there is some
remaining hysteresis in the prewetting transitions, but not in the position
of the KT line. Prewetting is in the 2D Ising universality class, and the
phase transitions in this type of system are well known to be strongly
affected by disorder [31-34], while the KT transition, which is in the
XY universality class, is relatively insensitive to disorder [35].
 The junction in the
m-T plane of the first order prewetting line
and the higher order KT line shown in Figure 4 has an unusual topology.
Model calculations [36,37] show that the junction between a first order
and higher order transition at a tricritical point usually occurs with
no change in slope. Although the connection between the reverse transition
(spinodal) and the KT line does appear to be smooth, the KT line meets
the forward transition in a sharp, cusp-like angle. Cusp-like junctions
in which the two transition lines meet tangentially are also allowed
[38, 39]. The junction in the
m-T plane of the first order prewetting line
and the higher order KT line shown in Figure 4 has an unusual topology.
Model calculations [36,37] show that the junction between a first order
and higher order transition at a tricritical point usually occurs with
no change in slope. Although the connection between the reverse transition
(spinodal) and the KT line does appear to be smooth, the KT line meets
the forward transition in a sharp, cusp-like angle. Cusp-like junctions
in which the two transition lines meet tangentially are also allowed
[38, 39].
 Previous investigators
have reached differing conclusions on the behavior of the superfluid onset
transition at low temperatures. Demolder et al. [11] analyzed their results
using an extrapolation scheme that properly accounted for the temperature
dependences of the leading thermodynamic terms and concluded that the superfluid
onset line does not intersect bulk liquid - vapor coexistence at a finite
temperature. Wyatt et al. [13] studied mass transport across a Rb surface
for 0.1K<T<0.35K in a region very close to coexistence (Dm<0.006K).
They interpret a jump in the critical superflow velocity to indicate a
wetting temperature just above 0.3 K where a prewetting line joins the
bulk liquid - vapor coexistence line. In terms of the surface energy balance,
the difference between a 0.3 K wetting temperature and T = 0 K prewetting
is minuscule and might easily be due to very small differences in the surface
chemistry [40]. Wyatt et al. also suggest that both the thin and thick
films along the prewetting lines are superfluid. In contrast, all of the
Rb surfaces we investigated were wet at coexistence. Furthermore, the dissipation
peak which is the hallmark of the KT transition was observed only in the
thick phase. The behavior in the thin phase undergoes a subtle continuous
change near T=0.3K, which does not resemble the standard signature of either
a superfluid onset transition or a first order transition with a discontinuity
in the film thickness. Previous investigators
have reached differing conclusions on the behavior of the superfluid onset
transition at low temperatures. Demolder et al. [11] analyzed their results
using an extrapolation scheme that properly accounted for the temperature
dependences of the leading thermodynamic terms and concluded that the superfluid
onset line does not intersect bulk liquid - vapor coexistence at a finite
temperature. Wyatt et al. [13] studied mass transport across a Rb surface
for 0.1K<T<0.35K in a region very close to coexistence (Dm<0.006K).
They interpret a jump in the critical superflow velocity to indicate a
wetting temperature just above 0.3 K where a prewetting line joins the
bulk liquid - vapor coexistence line. In terms of the surface energy balance,
the difference between a 0.3 K wetting temperature and T = 0 K prewetting
is minuscule and might easily be due to very small differences in the surface
chemistry [40]. Wyatt et al. also suggest that both the thin and thick
films along the prewetting lines are superfluid. In contrast, all of the
Rb surfaces we investigated were wet at coexistence. Furthermore, the dissipation
peak which is the hallmark of the KT transition was observed only in the
thick phase. The behavior in the thin phase undergoes a subtle continuous
change near T=0.3K, which does not resemble the standard signature of either
a superfluid onset transition or a first order transition with a discontinuity
in the film thickness.
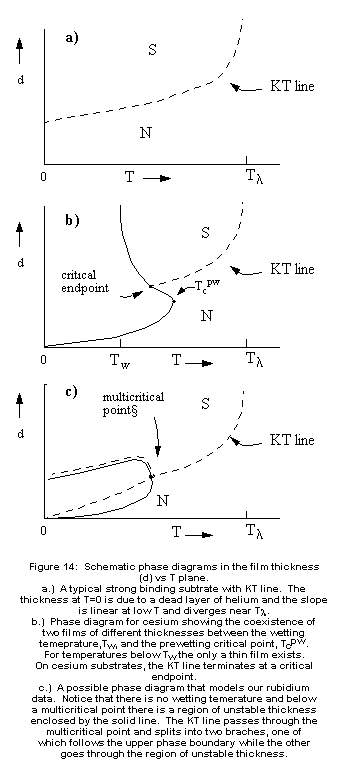  It
is useful to compare the superfluid transition observed on Rb with superfluid
onset on conventional substrates and Cs, as shown in the schematic d-T
phase diagrams shown in Figure 14. Figure 14a shows the phase diagram for
4He adsorbed on a conventional substrate such as mylar or gold.
The helium film exists in only two states, superfluid (S) and normal (N),
which are separated by the dashed KT line. The d>0 intercept at T=0 corresponds
to the dead layer. The linear dependence of d on T at low temperature is
very similar to that given by Eq. 2, while the divergence at Tl is due
to finite size effects, with . Figure 14b shows the combined prewetting
/superfluid onset phase diagram for 4He on Cs. Cs substrates
thicker than approximately 3 layers have a wetting temperature Tw>0.
For 0<T<Tw, a thin phase can coexist with bulk liquid.
For Tw<T<Tcpw, there is a range
of film thickness which is unstable. The KT line is almost exactly the
same as in Fig 14a, except that it terminates at a critical endpoint when
it collides with the range of unallowed d. For temperatures below the critical
endpoint, the signatures of the KT transitions are not observed [9], because
the film never attains the critical onset thickness. A candidate phase
diagram which summarizes our observations of superfluid onset on Rb is
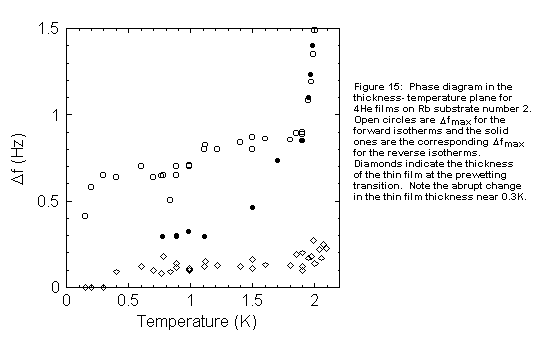
shown in Figure 14c, which should be compared to the data in Figure 15.
In this case, there is no wetting temperature, but there is a prewetting
transition, which corresponds to a range of unstable thickness. The hysteresis
we observe is due to metastable states between the phase boundary and the
spinodal line. On the forward isotherms, the transition takes place at
the upper phase boundary, while on the reverse isotherms, the transition
takes place on the lower spinodal line. Where the spinodal line and the
phase boundary meet marks the end of hysteresis at a critical point. In
this case, however, the KT line intersects the prewetting phase boundary
very close to the prewetting critical point. Since both the thickness and
the superfluid order parameter are singular there, it is presumably a multicritical
point. The resulting phase diagram resembles the well known bulk 3He-4He
mixture phase diagram (with d playing the role of 4He
concentration) which also has a multicritical point where the lambda line
hits the phase separation curve. It
is useful to compare the superfluid transition observed on Rb with superfluid
onset on conventional substrates and Cs, as shown in the schematic d-T
phase diagrams shown in Figure 14. Figure 14a shows the phase diagram for
4He adsorbed on a conventional substrate such as mylar or gold.
The helium film exists in only two states, superfluid (S) and normal (N),
which are separated by the dashed KT line. The d>0 intercept at T=0 corresponds
to the dead layer. The linear dependence of d on T at low temperature is
very similar to that given by Eq. 2, while the divergence at Tl is due
to finite size effects, with . Figure 14b shows the combined prewetting
/superfluid onset phase diagram for 4He on Cs. Cs substrates
thicker than approximately 3 layers have a wetting temperature Tw>0.
For 0<T<Tw, a thin phase can coexist with bulk liquid.
For Tw<T<Tcpw, there is a range
of film thickness which is unstable. The KT line is almost exactly the
same as in Fig 14a, except that it terminates at a critical endpoint when
it collides with the range of unallowed d. For temperatures below the critical
endpoint, the signatures of the KT transitions are not observed [9], because
the film never attains the critical onset thickness. A candidate phase
diagram which summarizes our observations of superfluid onset on Rb is
shown in Figure 14c, which should be compared to the data in Figure 15.
In this case, there is no wetting temperature, but there is a prewetting
transition, which corresponds to a range of unstable thickness. The hysteresis
we observe is due to metastable states between the phase boundary and the
spinodal line. On the forward isotherms, the transition takes place at
the upper phase boundary, while on the reverse isotherms, the transition
takes place on the lower spinodal line. Where the spinodal line and the
phase boundary meet marks the end of hysteresis at a critical point. In
this case, however, the KT line intersects the prewetting phase boundary
very close to the prewetting critical point. Since both the thickness and
the superfluid order parameter are singular there, it is presumably a multicritical
point. The resulting phase diagram resembles the well known bulk 3He-4He
mixture phase diagram (with d playing the role of 4He
concentration) which also has a multicritical point where the lambda line
hits the phase separation curve.
 The fact that the
standard signatures of a KT transition (superfluid jump and dissipation
peak) are observed all along the prewetting line implies that the KT line
does not stop at the multicritical point, but rather continues along the
upper phase boundary and along the spinodal. This is surprising because
the physics which determines the prewetting behavior and the superfluid
transition is ordinarily quite distinct, and it is not obvious why the
two transitions should not be completely independent. Apparently, on Rb
the combination of the multicritical point and the substrate disorder merge
the two phenomena into a single strongly coupled transition. The fact that the
standard signatures of a KT transition (superfluid jump and dissipation
peak) are observed all along the prewetting line implies that the KT line
does not stop at the multicritical point, but rather continues along the
upper phase boundary and along the spinodal. This is surprising because
the physics which determines the prewetting behavior and the superfluid
transition is ordinarily quite distinct, and it is not obvious why the
two transitions should not be completely independent. Apparently, on Rb
the combination of the multicritical point and the substrate disorder merge
the two phenomena into a single strongly coupled transition.
 Although the positions
of the features which mark the surface phase transitions are quite reproducible
from one Rb sample to another, the size and shape of the features vary
considerably, and as noted above, cannot be simply explained by the standard
KT model. The discrepancies in the superfluid jump are particularly puzzling
since the predicted value, which is universal, has been experimentally
verified on a number of substrates. It should be noted that in any oscillator
experiment, particularly at low temperature, a potential source of error
in measurements of df is the superfluid coupling factor k of Eq 1. In systems
in which k approaches 1 such exfoliated graphite studied in [21], the observed
values of df are very small because the oscillator
couples to almost all of the fluid even when it is superfluid. The data
can be corrected for this effect by multiplying the observed values of
df by 1/(1-k). The values of the superfluid
jumps corrected using this procedure agree with the KT prediction even
for exfoiliated graphite, where the correction can be as large as a factor
of 50 [21]. We have not applied such a correction to our Rb data, (equivalent
to choosing k=0 on Rb) so the values of df shown
in Figures 3 and 7 are lower bounds. It is interesting to note that even
this lower bound for df is often considerably
larger than the KT prediction. Although the positions
of the features which mark the surface phase transitions are quite reproducible
from one Rb sample to another, the size and shape of the features vary
considerably, and as noted above, cannot be simply explained by the standard
KT model. The discrepancies in the superfluid jump are particularly puzzling
since the predicted value, which is universal, has been experimentally
verified on a number of substrates. It should be noted that in any oscillator
experiment, particularly at low temperature, a potential source of error
in measurements of df is the superfluid coupling factor k of Eq 1. In systems
in which k approaches 1 such exfoliated graphite studied in [21], the observed
values of df are very small because the oscillator
couples to almost all of the fluid even when it is superfluid. The data
can be corrected for this effect by multiplying the observed values of
df by 1/(1-k). The values of the superfluid
jumps corrected using this procedure agree with the KT prediction even
for exfoiliated graphite, where the correction can be as large as a factor
of 50 [21]. We have not applied such a correction to our Rb data, (equivalent
to choosing k=0 on Rb) so the values of df shown
in Figures 3 and 7 are lower bounds. It is interesting to note that even
this lower bound for df is often considerably
larger than the KT prediction.
 The KT predictions
for the dissipation are not universal, although the dissipation is expected
to be proportional to the temperature [3]. This trend has been observed
in systems with thick helium films at relatively high temperature [4, 18],
but experiments at lower temperature [25, 21] show anomalies in both the
height and the width of the peaks which can not be explained by the standard
theory [3]. Dissipation measurements using an oscillating substrate are
subject to the same corrections for the superfluid coupling factor as discussed
above, so our values of DR again represent a
lower bound. The KT predictions
for the dissipation are not universal, although the dissipation is expected
to be proportional to the temperature [3]. This trend has been observed
in systems with thick helium films at relatively high temperature [4, 18],
but experiments at lower temperature [25, 21] show anomalies in both the
height and the width of the peaks which can not be explained by the standard
theory [3]. Dissipation measurements using an oscillating substrate are
subject to the same corrections for the superfluid coupling factor as discussed
above, so our values of DR again represent a
lower bound.
|
|




